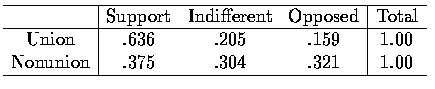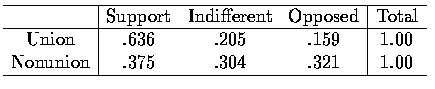Descriptive Study of Bivariate Data 二元資料簡介

在上一章中, 我們看到的例子都是屬於單一變數的問題, 但在日常生活上, 常見到的例子都是兩個(bivariate) 或是多個變數(multivariate)以上的, 而我們對於兩個變數間的關係(relation)特別有興趣. 現在只考慮兩個變數, 例子如下,

    大學畢業生中, 性別與選擇的工作職業之間的關係關係
    在成年男性中, 抽煙習慣與肺癌嚴重程度之間的關係
    10 歲大的兒童中, 每天平均碳水化合物與蛋白質的攝取量之間的關係
    飛機的機齡與需要維修的時數之間的關係

Bivariate Categorical Data

When two traits are observed for the individual sampling units and each trait is recorded in some qualitative categories, the resulting data can be summarized in the form of a two-way frequency table. The categories for one trait are marked along the left margin, those for the other along the upper margin, and the frequency counts recorded in the cells. Data in this summary form are commonly called cross-classified or cross-tabulated data. In statistical terminology, they are also called contingency tables.

例 1

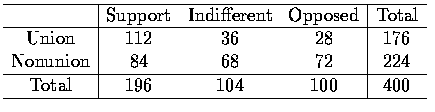
A survey was conducted by sampling 400 persons who were questioned regarding union membership and attitude toward decreased national spending on social welfare programs. The cross-tabulated frequency counts are presented as follow. To gain further understanding of how the responses are distributed, calculate the relative frequencies of the cells

Table 1 Cross-Tabulated Frequency Counts

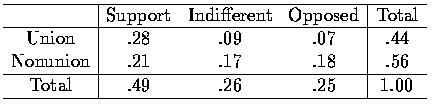
For this purpose, we divide each cell frequency by the sample size 400. The relative frequencies (for instance, 84/400=.21) are shown in Table 2.

Table 2 Relative Frequencies for the Data of Table 1

From the calculations in Table 3, it appears that the attitude patterns are different between the two groups - support seems to be stronger among union members than nonmembers.

Table 3 Relative Frequencies by Group