變異量數 Measures Of Variation
在統計中, 我們關心的不只是數據的中心值落於何處, 對於其分布的集中情形也有興趣,
因為兩個不同的資料可能有相同的中心, 或是中心相當的接近,
但我們可以由它們的所對應的變異情況來區分其不同的性質,
在這節中將介紹一些常用的測度來比較資廖組中的變異程度.
- Deviation 離差
- 若有
x1,x2,...,xn n 個觀測值,
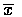 為它們的平均,
則它們的中心離差 deviations from the mean 分別為,
為它們的平均,
則它們的中心離差 deviations from the mean 分別為,
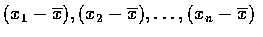 ,簡稱離差 deviations. 離差和為 0,
,簡稱離差 deviations. 離差和為 0,
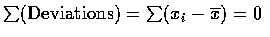
- Sample Variance 樣本變異數
- 若有
x1,x2,...,xn n 個觀測值,
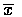 為它們的平均,
則它們的樣本變異數為
為它們的平均,
則它們的樣本變異數為
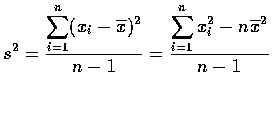 雖然, 樣本變異數 s2 為離差的平方後取平均,
但其自由度 (degree of freedom) 卻為 (n-1).
雖然, 樣本變異數 s2 為離差的平方後取平均,
但其自由度 (degree of freedom) 卻為 (n-1).
- Sample Standard Deviation 樣本標準差
-
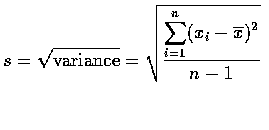
- 例 1
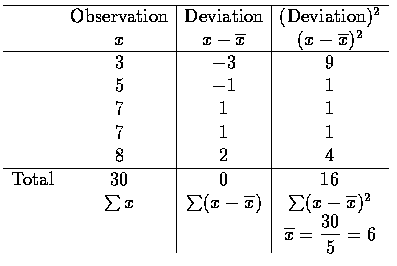
- 若有一組資料為: 3,5,7,7,8, 則它的樣本變異數與標準差如下
Sample variance
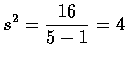
Sample Standard Deviation
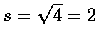
- 例 2
- 某心理測驗中, 有六個受測體接受某一固定強度的刺激信號試驗.
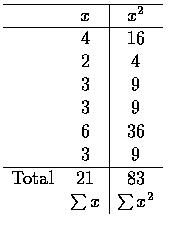
他們的反應時間分別為 4,2,3,3,6,3 (秒). 則他們的平均與標準差如下,
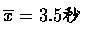
![$\displaystyle s^2=\frac{1}{n-1}[\sum x^2 - \frac{(\sum x)^2}{n}]=\frac{83-(21)^2/6}{5}=
\frac{83-73.5}{5}=\frac{9.5}{5}=1.9$](img12.gif)
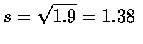
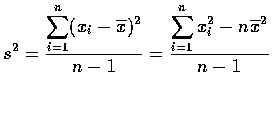 雖然, 樣本變異數 s2 為離差的平方後取平均,
但其自由度 (degree of freedom) 卻為 (n-1).
雖然, 樣本變異數 s2 為離差的平方後取平均,
但其自由度 (degree of freedom) 卻為 (n-1).
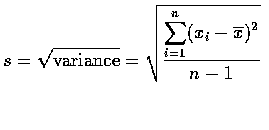
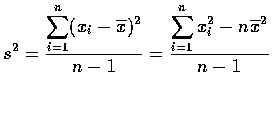 雖然, 樣本變異數 s2 為離差的平方後取平均,
但其自由度 (degree of freedom) 卻為 (n-1).
雖然, 樣本變異數 s2 為離差的平方後取平均,
但其自由度 (degree of freedom) 卻為 (n-1).
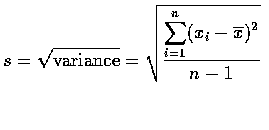
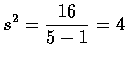
![$\displaystyle s^2=\frac{1}{n-1}[\sum x^2 - \frac{(\sum x)^2}{n}]=\frac{83-(21)^2/6}{5}=
\frac{83-73.5}{5}=\frac{9.5}{5}=1.9$](img12.gif)