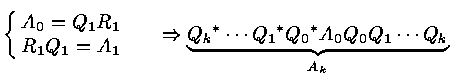
Chapter 5.2 Subspace Iteration , Simutaneous Iteration and the QR Algerithm
QR Algerithm
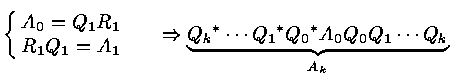
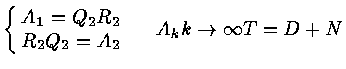
Power Method A : Simple
![]()
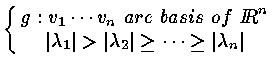
![]()
then
![]()
If
![]() are two subspace of Fn
are two subspace of Fn
define 1.
![]() 2.
2.
![]()
[Thm 5.2.2 ]
![]() simple with linear Indep. Eigenvectors
simple with linear Indep. Eigenvectors
![]()
with Eigenvalue
![]() Subspace
Subspace
![]()
for some k . Let
![]() and
and
![]()
Let ![]() be any k-dimensional subspace of Fn such that
be any k-dimensional subspace of Fn such that
![]() .
.
Then there exists a constant C
s.t.
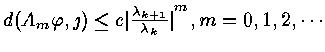
Thus ,
![]() linear with con. ratio
linear with con. ratio
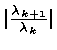
![]() linear if x_n+1 - x^* c x_n - x^* ifc < 1)
linear if x_n+1 - x^* c x_n - x^* ifc < 1)
Subspace Iteration
![]()
If ![]() : k-dim subspace
: k-dim subspace
![]() linear
linear
![]() ( Note :
( Note :
![]() are not all equal to 0 )
are not all equal to 0 )
![]()
If vi's are eigenvectors
![]()
![]() Am q =
Am q =
![]() because Aq =
because Aq =
![]()
=
![]()
=
![]()
Support that
![]()
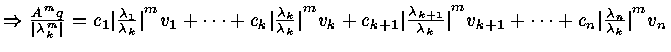
QR Algorithm
A = A0
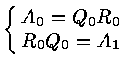
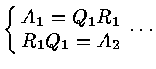
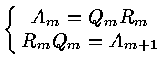
![]() Am+1 =
Am+1 =
![]()
Am+1
![]()
![]() Q* A Q = T = D + N ( In complex field )
Q* A Q = T = D + N ( In complex field )
=
![$\left [ \matrix{ T_{11} & T_{12} & \cdots & T_{1n} \cr
& T_{22} & \cdots & \vdots \cr && \ddots & \vdots \cr
0 &&& T_{pp} \cr } \right ]$](img41.gif) ( In real field )
( In real field )
Recall that
If
x = [ x1 , x2 ] ,
![]() ,
,
![]()
hen
B = x-1 A x =
![$\left [ \matrix{ B_{11} & B_{12} \cr 0 & B_{22} \cr } \right ]$](img44.gif)
![]()
![]()
For
![]()
![]()
![]()
![]()
QR Algorithm
[Thm 5.2.2 ] A is simple ,
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]() for some k
for some k
Assume
![]()
then ![]() s.t.
s.t.
![]()
![]()
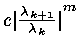
i.e.
![]() linear with conv. rate
linear with conv. rate
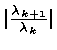 Note :
1. If
Note :
1. If
![]() then
then
![]() for all i
for all i
where
![]() provided that
provided that
![]() 2.
< v1 > = < q1 > < v1 , v2 > = < q1 , q2 > 3. If
2.
< v1 > = < q1 > < v1 , v2 > = < q1 , q2 > 3. If
![]() holds for all k
holds for all k
( The process of orthogonal can used by 1. Gram Schmidt process
or 2.
![]() )
)
Simultaneous Iteration
Let ![]() be a k-dimensional subspace of Fn with basis
be a k-dimensional subspace of Fn with basis
![]()
Assume that
![]()
![]()
Let
![]() be the i-dimensional subspace spanned by
be the i-dimensional subspace spanned by
![]()
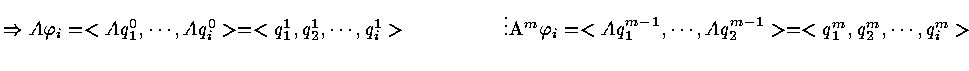
If
![]()
![]() provided
provided
![]() ( mean that success for
( mean that success for
![]() )
)
Note : i can be moving , just apply the above reservation .
Note : success for some i , and success for all ![]()
(*) If
![]() , for all
, for all
![]()
then
![]()
true for all
![]()
The mth step of the QR algorithm
![]() , where
, where
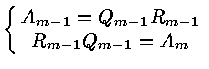
![]() are ON
are ON
Now ,
![]()
provided
![]()
because If m is large
![]()
If
![]()
![$\Rightarrow A_{m+1} = \left [
\matrix{ A_{11} & A_{12} \cr
0 & A_{22} \cr
}
\right ]$](img86.gif)
![$A_m = {\hat Q}_m A Q_m \approx \left [
\matrix{ A^{(m)}_{11} & A^{(m)} \cr
0 & A^{(m)}_{22} \cr
}
\right ]$](img87.gif)
m is lagre , Qm first k column
![]()
1. Simultaneous Iteratons :
![]() 2. QR Algerithm
2. QR Algerithm
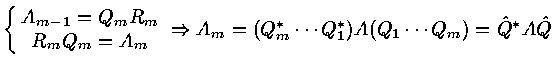
![]() are the standard basis vectors
are the standard basis vectors
![]()
If
![]() then
then
![]() ( Note :
( Note :
![]() )
)
Note : If
![]() are column vectors of A
are column vectors of A
If
![]()
then qi's are the orthonormalized vectors of ai's
Letting
![]() , we have
A = Q1 R1
, we have
A = Q1 R1
The unitary transformation of A
![]()
![]() . This constitute the 1th step of QR iteration
. This constitute the 1th step of QR iteration
Note : 2th step , the relation of QR and Simultaneous Iteration
![]() ( where
( where
![]() ,
the matrix after orthogonal )
=
,
the matrix after orthogonal )
=
![]()
because
![]() x in origion A , and
x in origion A , and
![]() in A1
in A1
( the origion coordinate system ) ( the new coordinate system )
origion
![]() ,
new
,
new
![]()
=
![]()
![]()
![]() equivalent to
A1 I = A1 and
equivalent to
A1 I = A1 and
![]() equivalent to
A1 = Q2 R2
equivalent to
A1 = Q2 R2
Field , ![]() , C
, C
Addition: 1. associate 2. commutation 3. exists unit element 4. exists inverse element
Multiplication : 1. associate 2. commutation 3. exists unit element 4. exists inverse element
Note : The field that Q is minimal
Example 1. : z is not a subfield of C
Example 2. :
![]() is a subfield of C
is a subfield of C
Vector Space [Def] A vector space consists of the following :
1. F2. v ( vectors ) 3. A rule is called vector addition and multipication Rule that satisty "Addition" :
a. associate
b. commutation
c. unit element ( 0 )
d. inverse element ( ![]() )
)
Example : The space of all
![]() matrix
( Addition :
[A+B]ij = Aij + Bij)
matrix
( Addition :
[A+B]ij = Aij + Bij)
The relation of F and v must satisfy :
e.
![]() f.
f.
![]() g.
g.
![]() h.
h.
![]()
Vector space over
![]()
Subspace :
v : vector space
If w is a subset of v then w is a subspace of v
if w itself a vector space
( must satisfy the rule that define by v )
[Thm] A nonempty subset w of v is a subspace of v
if and only if
![]()
![]()
![]()
Example :
![]() is Hermition is not a subspace over C
is Hermition is not a subspace over C
but it is a subspace over ![]()
( Note : The set of all
![]() complex Hermition matrices is not
complex Hermition matrices is not
a subspace over c but in a subspace over ![]() )
Span
[Def] S be a set of vectors in a vector space v
)
Span
[Def] S be a set of vectors in a vector space v
The subspace span by S is defined to be the
intersection of all subspace v which contains S
![]()
![]() , w is subspace contains S
, w is subspace contains S
![]() , where
, where
![]() . w : subspace
. w : subspace
Bases and Dimension :
[Def] A set S of v ( vector space ) is linear dependent if
there exists distinct vectors
![]() in S ,
in S ,
and scalars
![]() not all of which are 0 ,
not all of which are 0 ,
such that
![]()
A set which is not linearly dependent is called linear Independent
Example : If A set contain the vector 0 must be linear dependent .
[Def] Let v be a vector space . A basis for v is a
linear indep. set of vectors in v which span v
Example :
![]()
![]() , Bi are column vectors .
, Bi are column vectors .
![]()
AB = C , C =
![$\left [ \matrix{ {\gamma}_1 \cr {\gamma}_2 \cr \vdots \cr {\gamma}_n } \right ]$](img134.gif)
![]() are row vectors of C
are row vectors of C
![]() are row vectors of B
are row vectors of B
AB = C
![]() =
=
![]() for all i
for all i
Order Basis
Example :
![]() ,
,
![]()
![]() ( x1 , x2 , x3 ) =
( x1 , x2 , x3 ) =
![]()
![]()
![$ {[ \alpha ]}_{\beta} =
\left [ \matrix{ x_1 \cr x_2 \cr x_3 \cr } \right ]$](img144.gif)
Example :
![]()
![]() =
=
![$\left [ \matrix{ x_1 \cr x_2 \cr } \right ]$](img147.gif)
( x1 , x2 ) = x1 ( 1,0 ) + x2 ( 0.1 )
(*) B' =
![]()
![]() =
( x'1 , x'2 )
=
( x'1 , x'2 )
![]() =
=
![]()
![]()
B' =
![]()
![]()
![]() for all iPij exists and only
for all iPij exists and only
![]() =
=
![]() where
P = [ Pij ]
where
P = [ Pij ]
![]() if and only if x=0
if and only if x=0
![]() is invertible and
is invertible and
![$\left \{ \matrix{ {[ \alpha ]}_{{\beta}^{\prime}}$\space =
$ P {[ \alpha ] }_{...
...\alpha ]}_{{\beta}}$ =
$ P^{-1} {[ \alpha ] }_{{\beta}^{\prime}} \cr } \right $](img157.gif)
![]()
![]()
![$\left [ \matrix{ ( \cos \theta , \sin \theta ) = \cos (1,0) + \sin (0.1) \cr
( - \sin \theta , \cos \theta ) = - \sin (1,0) + \cos (0,1) \cr }
\right ]$](img160.gif)
so
![]() =
=
![]() where P =
where P =
![$\left [\matrix{ \cos \theta & - \sin \theta \cr \sin \theta & \cos \theta \cr
}\right ]$](img161.gif)
![$\left [ \matrix{ {x^{\prime}_1} \cr {x^{\prime}_2} \cr } \right ]$](img162.gif) =
=
![$\left [\matrix{ \cos \theta & - \sin \theta \cr \sin \theta & \cos \theta \cr
}\right ]$](img161.gif)
![$\left [ \matrix{ x_1 \cr x_2 \cr } \right ]$](img147.gif)
![]()
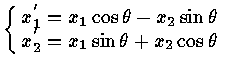
![]()
![]() , T exists and only
, T exists and only
![$ P^{-1} = \left [
\matrix{ \cos \theta & \sin \theta \cr
- \sin \theta & \cos \theta \cr
}
\right ]$](img166.gif)
![]() =
=
![]() =
=
![$\left [ \matrix{ x_1 \cr x_2 \cr } \right ]$](img147.gif)
![]()
![$\left [ \matrix{ x_1 \cr x_2 \cr } \right ]$](img147.gif) =
=
![$\left [ \matrix{ \cos \theta & \sin \theta \cr
- \sin \theta & \cos \theta \cr } \right ]$](img169.gif)
![$\left [ \matrix{ y_1 \cr y_2 \cr } \right ] \Rightarrow {\beta}^'$](img170.gif) can find (*)
can find (*)
Linear Transformation
![]() is a function
is a function
s.t.
![]()
Then T is called Linear Transformation from v into w .
Example :
![]() then 1. T most through zero point
2. T must be linear function
then 1. T most through zero point
2. T must be linear function
T (0) = 0 because T(0+0) = T(0) + T(0)
![]() T(0) = T(0) + T(0)
T(0) = T(0) + T(0)
![]() T(0) = 0
T(0) = 0
Fact : rank(T) + nullity(T) = dim v
[Thm]
![]() linear transformation , then
linear transformation , then
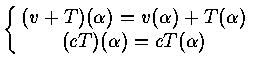
L ( v , w ) : the set of all linear transformations
then L ( v , w ) is a vector space .
Note : dim L ( v , w ) = ( dim v ) ( dim w )
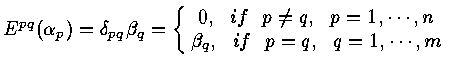
![]()
![]()
[Def]
![]() , then T is called the linear operator on v
, then T is called the linear operator on v
![]() is invertible if there is a
is invertible if there is a
![]() s.t.
s.t.
Tv = I = vT , v = T-1 ( or T = v-1 )
T is invertible iff 1. T is 1-1
![]() null space = { 0 }
2. T is onto
null space = { 0 }
2. T is onto
A is nonsingular ( Invertible ) if A-1 exist iff
![]()
T is nonsingular off
![]()
If T is 1-1 or onto ?
if
![]()
because
![]()
T is nonsingular
![]()
onto ( by
rank(T) + nullity(T) = dim v )
![]()
![$\left
\matrix{ {[ \alpha ]}_{\beta } = P {[ \alpha ]}_{\beta } \cr
\Rightarro...
... \alpha ]}_{{\beta }^{\prime}} = P^{-1} {[ \alpha ]}_{\beta } \cr
}
\right \}$](img187.gif) where
where
![]()
![]()
![]() order basis for v
order basis for v
![]() order basis for w
order basis for w
![]() , for all
, for all
![]()
A = ( Aij ) is called the matrix T relative to the pair
of order basis ![]() and
and ![]()
If
![]() , then
, then
![]()
![]() =
=
![]() =
=
![]() =
=
![]() =
=
![]()
![]()
![]() =
=
![]()
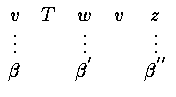
![$\left
\matrix{ {[T]}_{ \beta \rightarrow {\beta}^{\prime} } = A \cr
{[v]}_{ {\beta}^{\prime} \rightarrow {\beta}^{\prime \prime} } = B \cr
}
\right \}$](img205.gif)
![]()
( the Multiplication of
![]() the combine of linear transformation )
the combine of linear transformation )
![]()
![]()
Example :
![]() field
field
T ( x1 , x2 ) = ( x1 , 0 ) ,
![]()
![]() =
T ( 1 , 0 ) = ( 1 , 0 ) =
=
T ( 1 , 0 ) = ( 1 , 0 ) =
![]()
![]()
![]()
![]()
![$\left [ \matrix{ 1 & 0 \cr 0 & 0 \cr } \right ] $](img217.gif)
![]() =
=
![]()
![]() =
=
![]() (
(
![]() =
=
![]() =
=
![]()
![]() =
=
![]()
( because
![]()
![]() =
=
![]()
![]() linear operators
linear operators
![]()
![]() =
=
![]() are ordered bases for v
are ordered bases for v
because
![]() =
=
![]() where
where
![$P_j = { [{{\alpha}^'_j}] }_{\beta} , P_j$](img230.gif) : the column vector of Pbecause
: the column vector of Pbecause
![]() =
=
![]() =
=
![]() now from (*) ( change by
now from (*) ( change by
![]() )
)
![]()
![]() =
=
![]()
![]()
![]() =
=
![]() =
=
![]()
![]()
![]() P =
P =
![]()