Chapter 5 Eigenvalue and Eigenvector II

5.1 Invariance Subspace

F : ( C or $I\!\!R$ ) a field

<Def> A subspace $\varphi \leq F^n$ is invariant ( of A )

if $Ax \in \varphi$ , where $x \in \varphi$

Example : 1. If v is Eigenvector of A <v> the eigenspace of A

then <v> is invariant .

$\Rightarrow$ $u \in <v>$ $\Rightarrow$ u = c u $\Rightarrow Au$ = $\lambda u \in <v>$

2. $N ( \lambda I - A )$ : the null space of $\lambda I - A$

<Thm 5.5.1>

Let $\varphi$ be a subspace of Fⁿ with basis $x_1 x_2 \cdots x_k$

Thus $\varphi = < x_1 , \cdots , x_l >$ Let $\hat x = [ x_1 \cdots \x_k ] \in F^{ n \times k }$

Then $\varphi$ is invariant under $A \in F^{ n \times n }$

$\Leftrightarrow$ there exist $\hat B \in F^{k \times k } \ni A \hat x = \hat x B$

Recall that $A \in C^{ n \times n } , x \in C^{ n \times k } , B \in C^{ k \times k }$

Ax = xB $\Leftrightarrow R(x)$ is invariant and $\lambda (A) = \lambda (B)$

Schur's Thm : $A \in C^{ n \times n }$ , $\exists Q$ unitary s.t. Q^* A Q = T = D + N

Real Shur's Thm : $A \in {I\!\!R}^{n \times n}$ , $\exists u$ orthogonal $\ni v^T A v = T$

$T = \left [ \matrix{ T_{11} & T_{12} & \cdots & T_{1n} \cr & T_{22} & \cdots & \vdots \cr && \ddots & \vdots \cr 0 &&& T_{pp} \cr } \right ]$ where $T_{ii} \in {I\!\!R}^{ 1 \times 1 }$ or ${I\!\!R}^{ 2 \times 2 }$

$A \in C^{ n \times n } , B \in C^{ p \times p } , \exists x$ s.t. if $Ax = xB , \exists Q , \ni Q^* A Q = \left [ \matrix{ T_{11} & T_{12} \cr 0 & T_{22} \cr } \right ]$ and $\lambda (A) = \lambda (T_{11}) \cup \lambda (T_{22})$

<Thm 5.1.2 > Let $\varphi$ be invariant under $A \in F^{ n \times n }$ and Let $x_1 , \cdots , x$ be a basis for $\varphi$

Let $x_{k+1} , \cdots , x_n$ be any n - k vectors s.t. $x_1 , \cdots , x_k$

is a basis for Fⁿ . Let $x_1 = [x_1 , \cdots , x_k ] , x_2 = [x_{k+1} , \cdots , x_n ]$

and $x = [x_1 , x_2] \in F^{ n \times n }$

Define B = x^-1 A x , then B is block upper triangular $B = \left [ \matrix{ B_{11} & B_{12} \cr 0 & B_{22} \cr } \right ]$

Furthermore A x₁ = x₁ B

( $v \in < x_1 , \cdots , x_k >$ , xv = ${\sum}^n_{i=1} x_i$ = ${\sum}^k_{x=1} x_i + 0 \cdot x_{k+1} + \cdots + 0 \cdot x_n$ )

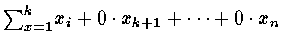Note : 1. $B = \left [ \matrix{ B_{11} & B_{12} \cr B_{21} & B_{22} \cr } \right ]$ If B₂₁ = 0 , then $\varphi$ is invariant 2. $x = [ x_1 , \cdots , x_k , \cdots , x_n ]$ can be a orthogonal matrix

Exercise 5.1.10 : If $\varphi$ is invariant under $A \Leftrightarrow {\varphi}^{\bot}$ is invariant under A^*

Note : If A is Hermitian ( A^* = A ) , then $\exists Q \rightarrow Q^* A Q = D$

[Real Schur's Thm] $A \sim \left [ \matrix{ T_{11} & T_{12} & \cdots & T_{1n} \cr & T_{22} & \cdots & \vdots \cr && \ddots & \vdots \cr 0 &&& T_{pp} \cr } \right ]$ $T_{ii} \in {I\!\!R}^{ 1 \times 1 }$ or ${I\!\!R}^{ 2 \times 2 }$

Note : 1. If $\lambda$ is an Eigenvalue of A , then $\tilde \lambda$ is also an Eigenvalue of A 2. v = v₁ + i v₂ is the Eigenvector of A $\~ v = v_i - i v_2$ is also the Eigenvector of A