Chapter 4.4 Similarity Transformation and Relative Topics

[Def] A $\sim$ B ( similar ) if $\exists$ P nonsingular s.t. A = P^-1 B P ( where $A , B \in C^{n \times n}$ )

[Thm] Similar matrices have the same Eigenvalues

<Proof> If $A \sim B \Rightarrow \exists P$ nonsingular s.t. A = P^-1 B P Consider ( $\lambda I - A$ ) = $det ( P^{-1} \lambda I P - P^{-1} B P )$ = $det [ P^{-1} ( \lambda I - B ) P ]$ = $( det P^{-1} )( det ( \lambda I - B ))( det P )$ = $det ( \lambda I - B ) det ( P^{-1} ) det ( P )$ = $det ( \lambda I - B ) det ( P^{-1} P )$ = $det ( \lambda I - B )$

[Thm] If v is an Eigenvector of A with associated Eigenvalues $\lambda$

If B = P^-1 A P , then (P^-1 V) is an Eigenvector of B with associated $\lambda$

<Proof> $A v = \lambda v$ , and B = P^-1 A P $\Rightarrow$ P B P^-1 v = $\lambda v \Rightarrow B ( P^{-1} v )$ = $\lambda ( P^{-1} v )$

[Def] $A \in C^{n \times n}$ is simple if the Eigenvectors of A form a basis for Cⁿ

[Def]

1. Algebraic multiplicity : if the characteristic polynomial of A is given by f(x) = ${( x - {\lambda}_1 )}^{d_1} {( x - {\lambda}_2 )}^{d_2} \cdots {( x - {\lambda}_k )}^{d_k}$

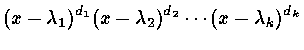
, then the order d_i is called the algebraic multiplicity of ${\lambda}_i$2. ${\varphi}_{{\lambda}_i}$ = $\{ v \vert Av = {\lambda}_i v \}$ , then the geometric multiplicity = $Rank ( {\varphi}_{{\lambda}_i} )$

Note : Geometric multiplicity $\leq$ Algebraic multiplicity

Example : $A = \left [ \matrix{ 1 & 0 \cr 0 & 1 \cr } \right ]$         Rank = $\left [ \matrix{ 0 & 0 \cr 0 & 0 \cr } \right ] = 0$Nullity = $\left [ \matrix{ 0 & 0 \cr 0 & 0 \cr } \right ] = 2$

Characteristic polynomial = ( x - 1 )²

( $\lambda = 1$ ) : Algebraic multiplicity = 2 : geometric multiplicity = 2

$B = \left [ \matrix{ 0 & 1 \cr 0 & 0 \cr } \right ]$

Characteristic polynomial = x²

: Algebraic multiplicity = 2

: geometric multiplicity = 1

[Thm] Similar Transformation preserve both the algebraic and geometric multiplicities

Companion matrix

$A = \left [ \matrix{ 0 & 1 &&& \cr & 0 & 1 && \cr && \ddots & \ddots & \cr &&& 0 & 1 \cr -a_0 & -a_1 & \cdots & \cdots & -a_{n-1} \cr } \right ]$then $det ( \lambda I - A )$ = ${\lambda}^n + a_{n-1} {\lambda}^{n-1} + \cdots + a_0 = P ( \lambda )$ ( Jodan Form , Rational Form )

[Thm] ( diagonalizable )

If $A \in C^{n \times n}$ is simple with l.I. eigenvectors $u_1 , u_2 , \cdots , u_n$

then there exists $u = [ u_1 , u_2 , \cdots , u_n ]$ where u_i are column vectors s.t. D = u^-1 A u , where D = $\left [ \matrix{ {\lambda}_1 && 0 \cr & \ddots & \cr 0 && {\lambda}_n \cr } \right ]$

( i.e. $A \sim D$ )

$\left \{ \matrix{ f(x) = {( x - 2 )}^4 {( x - 3 )}^3 \cr P(x) = {( x - 2 )}^2 {( x - 3 )}^2 \cr } \right$

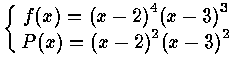
where f : characteristic poly. of A P : minimal poly. of A

Unitary Similary Transformation

A similar to B ( $A \sim b$ )

if $\exists P$ nonsingular

s.t. A = P^-1 B P

( $\Rightarrow PA = BP ~or~ Ax = xB , x = P^{-1}$ )

[Def] $v \in C^{ n \times n }$ is unitary if U U^* = I ( i.e. U^* = U^-1 )

where U^* is the conjugate transpose of U

Note 1.: If U unitary and $U \in {I\!\!R}^{ n \times n } \Rightarrow U$ is orthogonal

$A = \left [ \matrix{ 1+i & 3 \cr -2i & 1-i \cr } \right ] ~~~~ A^* = \left... ...ht ] = \left [ \matrix{ 1-i & 2i \cr 3 & 1+i \cr } \right ] \par\exists U$ unitary matrix , then A is unitary similary to B

( in ${I\!\!R}^{n \times n}$ is called orthogonal similary )

[Def] A is Hermite , if $A^* = A ( A \in C^{n \times n} )$

( in ${I\!\!R}^{n \times n}$ is called symmetric )

Note 2.: Unitary matrix have the same properties as the orthogonal matrix Example : (i.) (vx , vy ) = ( x , y ) = y^* x (ii.) ${\Vert vx \Vert}_2 = {\Vert x \Vert}_2$ (iii.) If $v_1 , v_2 , \cdots , v_n$ are unitary

$\Rightarrow ( v_1 , v_2 , \cdots , v_n )$ also unitary (iv.) A = VR ( the same to ${I\!\!R}^{n \times n}~~~A=QR$)

$A \in C^{n \times n} ~~ \lambda (A) =$ the set of all eigenvalues

If $\lambda (A)$ = $\{ {\lambda}_1 , {\lambda}_2 , \cdots , {\lambda}_n \}$

$\Rightarrow$ det (A) = ${\lambda}_1 {\lambda}_2 \cdots {\lambda}_n$ = ${\prod}^n_{i=1} {\lambda}_i$

t_r (A) = ${\sum}^n_{i=1} a_{ii} = {\sum}^n_{i=1} {\lambda}_i$

$Ax = xB , A \in C^{n \times n} , x \in C^{n \times k} , B \in C^{k \times k}$ S is invariant ( of A ) , if $x \in S \Rightarrow Ax \in S$

Note : x is eigenvector of A $\Rightarrow Ax = \lambda x$

( $\Rightarrow$ eigenspace of x is invariant ( of A ))

Note : If $Ax = xB \Rightarrow R(x)$ invariant

If ${\lambda}_i \in \lambda (B) \Rightarrow By = \lambda (y) \Rightarrow x (By) = A (xy) \par\Rightarrow \lambda (B) \subset \lambda (A)$

the same to $\Rightarrow \lambda (A) \subset \lambda (B) \Rightarrow \lambda (A) = \lambda (B)$

Ax = xB is called the Similary Transformation

( Note : If $x \in C^{n \times n}$ nonsingular $\Rightarrow B = x^{-1} A x$)

[Lemma] If $A \in C^{n \times n} , B \in C^{p \times p}$ satisfy $Ax = xB , x \in C^{n \times p}$ , then $\exists Q \in C^{n \times n}$ unitary s.t. $Q^* A Q = T = \left [ \matrix{ T_{11} & T_{12} \cr 0 & T_{22} \cr } \right ]$

Note : 1. $\lambda (A) = \lambda ( T_{11}) \cup (T_{22})$ 2. This Q is the Q of analysis x = QR

Example : $\left [ \matrix{ 67 & 177.60 & -63.20 \cr -20.40 & 95.88 & -87.16 \cr 22.80 & 67.84 & 12.12 \cr } \right ]$

$Q^T Q Q = T = \left [ \matrix{ 25 & -90 & 5 \cr 0 & 147 & -104 \cr 0 & 146 & 3 \cr } \right ]$

<Proof> $x = QR = Q {\left [ \matrix{ R \cr 0 \cr } \right ]}^P$ is the QR factorization of x

Because $Ax = xB \Rightarrow A Q \~ R = A \~ R B \Rightarrow Q^* A Q \left [ \matrix... ... \matrix{ R \cr 0 \cr } \right ] = \left [ \matrix{ R \cr 0 \cr } \right ]$

$T_{11} R = RB \par T_{21} R = 0 \par\Rightarrow T_{21} = 0$ ( because R is nonsingular )

[Schur's Theorem] If $A \in C^{n \times n}$ , then there exist Q unitray s.t. Q^* A Q = T = D + N , where D = $\left [ \matrix{ {\lambda}_1 && 0 \cr & \ddots \cr 0 && {\lambda}_n \cr } \right ]$ ${\lambda}_i$ are eigenvalues of A

Moreover ${\lambda}_i$ can be rearranged in any order

<Proof> (By Induction on n )

n = 1 ( get $B = \lambda$ ) ( $\Rightarrow x = \lambda x$ )

then from the Lemma $\exists v$ , unitary

s.t. $v^* A v = \left [ \matrix{ \lambda & w \cr 0 & c \cr } \right ]$ If the Thm is hold for all order $\leq$ n - 1

$\Rightarrow \exists \~ Q$ unitary s.t. ${\~ Q}^* c \~ Q = \~ T = \~ D + \~ N$

Let $Q = diag ( 1 , \~ Q ) = \left [ \matrix{ 1 & 0 \cr 0 & \~ Q \cr } \right ]$

then Q^* A Q = $\left [ \matrix{ \lambda & 0 \cr 0 & \~ T \cr } \right ]$ = T = D + N = $\left [ \matrix{ {\lambda}_1 && 0 \cr & \ddots \cr 0 && {\lambda}_n \cr } \right ]$

Example : $A = \left [ \matrix{ 75 & 200 \cr -50 & 75 \cr } \right ]$ then $Q = \left [ \matrix{ .8944i & .4472 \cr -.4722 & -.8944 \cr } \right ]$

Q^* A Q = T = $\left [ \matrix{ 75+100i & -150 \cr 0 & 75-100i \cr } \right ]$ = $\left [ \matrix{ 75+100i & 0 \cr 0 & 75-100i \cr } \right ] + \left [ \matrix{ 0 & -150 \cr 0 & 0 \cr } \right ]$

Note : If A is nonsingular $\Leftrightarrow$ N = 0

[Def] ${\Vert N \Vert}^2_F := {\Vert A \Vert}^2_F - {\sum}^n_{i=1} {\vert {\lambda}_i \vert}^2$ $\Rightarrow$ departure from nonsingularity

N is independent choice of Q

Note : Simple matrices are dense in ${I\!\!R}^{n \times n}$ ( or $C^{ n \times n }$ ) ( i.e. If A is choosen randomly $\Rightarrow$ slmost all A are simple )

If $\{ A_{\lambda} \}$ are simple matrices

$\Rightarrow$ for any $A \in C^{ n \times n} \exists {\{ A_n \}}^{\infty}_{n=1}$ s.t. $A^{n \rightarrow {\infty}}_n \rightarrow A ( \Vert A_n - A \Vert \rightarrow 0 )$

[Def] $A \in C^{n \times n}$ is said to be normal if A A^* = A^* A

[Thm] ( Spectral Thm for Normal Matrices )

$A \in C^{n \times n}$ is normal $\Leftrightarrow \exists Q$ unitary , s.t. Q^* A Q = D , D diagonal

<Proof> " $\Leftarrow$" Q^* A Q = D
D D^* = (Q^* A Q)(Q^* A Q)^* = Q^* A A^* Q

$\Rightarrow {\Vert Q D \Vert}^2_2$ = Q D D^* Q^* = A A^*

and ${( Q^* A Q)}^* (Q^* A Q) = A^* A = Q^* D^* Q D = {\Vert Q D \Vert}^2_2$

$\Rightarrow A A^* = A^* A$

" $\Rightarrow$" A is normal $\Rightarrow$ T is normal $\Rightarrow T T^* = T^* T \par\left \{ \matrix{ T = Q^* A Q \cr T^* = Q^* A^... ... ) Q \cr T^* T = Q^* ( A^* A ) Q \cr } \right \par\Rightarrow T T^* = T^* T$

${\Vert N \Vert}^2_F = {\Vert A \Vert}^2_F - \sum {\vert {\lambda}_i \vert}^2 = \bigtriangleup (N)$

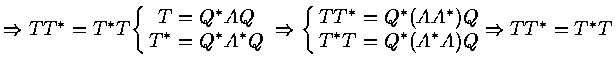
s called departure from the normality

A is normal if A A^* = A^* A

[Thm] A is normal $\Leftrightarrow \exists v$ unitary s.t. v^* A v = D

Note : 1. $\exists Q , \lambda . Q^* A Q = T = D + N$ ( Schur's Decomposition ) 2. ${\Vert QA \Vert}_F = {\Vert A \Vert}_F$

${\Vert A \Vert}_F = {( {\sum}_{ij} {\vert a_{ij} \vert}^2 )}^{ 1 \over 2 }$

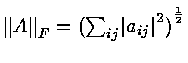
Example : $A = \left [ \matrix{ 1 & 2 \cr 3 & 4 \cr } \right ] ~~~~ {\Vert A \Vert}_F = \sqrt {1+4+9+16}$

Note : Simple matrices are dense in $C^{ n \times n }$ .

For all $A \in C^{ n \times n } , \varepsilon > 0 , \exists B$ is simple $\lambda \Vert A - B \Vert < \varepsilon$

Note : Matrices norm are equivalent , i.e. ${\Vert \cdot \Vert}_{\alpha} , {\Vert \cdot \Vert}_{\beta}$ are two matrices norm $\exists c_1 , c_2$ s.t. $c_2 {\Vert \cdot \Vert}_{\beta} \leq {\Vert \cdot \Vert}_{\alpha} \leq c_1 {\Vert \cdot \Vert}_{\beta}$

Note : $\bigtriangledown (N)$ is indep. of choice of Q . Q A Q = D + N

Example : $\overbrace {A \sim T}^{~unitary~similary} = \left [ \matrix{ 2 & 4 & 5 \cr 0 ... ... + \left [ \matrix{ 0 & 4 & 5 \cr 0 & 0 & 6 \cr 0 & 0 & 0 \cr } \right ]$ $A \sim T_1 = \left [ \matrix{ 2 & 1 & 0 \cr 0 & 2 & 0 \cr 0 & 0 & 3 \cr } \right ]$ ( Jordan Form of A )

Nonunitary Transformation

If $A \in C^{n \times n}$ , A = $\left [\matrix{ T_{11} & T_{12} \cr 0 & T_{22} \cr } \right ]$       p + q = n

[Def] $\varphi : C^{ p \times q }$ $\rightarrow$ $C^{ p \times q }$ s.t. $\varphi (x) = T_{11} x + x T_{22}$ , then $\varphi$ is nonsingular $\Leftrightarrow$ $\lambda ( T_{11}) \cap \lambda ( T_{22} ) = \varphi$

If $\varphi$ is nonsingular and Y is defined by $Y = \left [ \matrix{ I_p & z \cr 0 & I_q \cr } \right ]$

$\varphi (z) = - T_{12}$ , then Y^-1 A Y = $\left [ \matrix{ T_{11} & 0 \cr 0 & T_{12} \cr }\right ]$

[Thm] If A = $\left [ \matrix{ T_{11} & T_{12} & \cdots & T_{1n} \cr 0 & T_{22} && \vdots \cr \vdots && \ddots & \vdots \cr 0 & \cdots & \cdots & T_{nn} \cr } \right ]$, $\exists$ Y s.t. (YQ)^-1 A (YQ)= $\left [\matrix{ T_{11} &&& 0 \cr & T_{22} && \cr && \ddots & \cr 0 &&& T_{nn} \cr } \right ]$

where T_ii are square and $\lambda (T_{ii}) \cap \lambda (T_{jj})$ = $\varphi$ for all $i \ne j$

[Cor] If $A \in C^{n \times n}$ , then $\exists$ x nonsingular s.t. x^-1 A x = $diag ({\lambda}_1 I + N_1 , {\lambda}_2 I + N_2 , \cdots , {\lambda}_p I + N_p)$

where all ${\lambda}_i$ are distinct $N_i \in C^{n_i \times n_i}$

the integer $n_1 + n_2 + \cdots + n_p = n$

Note : n_i is the algebraic multipicity of ${\lambda}_i$

If $x = [ x_1 , x_2 , \cdots , x_p ]$ , then Range(x_i) are invariant subspace

$\Rightarrow$ $C^n = Range (x_1) \oplus Range (x_2) \oplus \cdots \oplus Range (x_p)$

Jordan's Block : J_i = $\left [ \matrix{ {\lambda}_1 & 1 &&&& 0 \cr & \ddots & \ddots &&& \cr && {\l... ...ddots & \ddots & \cr &&&& \ddots & 1 \cr 0 &&&&& {\lambda}_1 \cr } \right ]$

$c.f.~~~~{\lambda}_1 I + N_1$ = $\left [ \matrix{ {\lambda}_1 & \ddots & * & * & * \cr & {\lambda}_1 & \ddots... ...s & \ddots & * \cr &&& \ddots & \ddots \cr 0 &&&& {\lambda}_1 \cr }\right ]$Note : Transformation is called "nonunitary transformation" .

Example : $A \in {I\!\!R}^{7 \times 7 }$ , f(x) = ( t - 2 )⁴ ( t - 3 )³ , P(x) = ( t - 2 )² ( t - 3 )³

Jordan Form :

J₁ = $\left [ \matrix{ 2 & 1 &&&&& \cr 0 & 2 &&&& 0 & \cr && 2 & 1 &&& \cr && 1 & 2 &&& \cr &&&& 3 & 1 & \cr & 0 &&& 0 & 3 & \cr &&&&&& 3 \cr } \right ]$

J₂ = $\left [ \matrix{ 2 & 1 &&&&& \cr 0 & 2 &&&&& \cr && 2 &&&& \cr &&& 2 &&& \cr &&&& 3 & 1 & \cr &&&& 0 & 3 & \cr &&&&&& 3 \cr } \right ]$

the eigenspace of $J_1 ( w , r , t ~~ \lambda = 2 ) = 2$

the eigenspace of $J_2 ( w , r , t ~~ \lambda = 2 ) = 3$

Localized Eigenvalues and Derturbation

Gershgorin Circles : D_i = $\{ z \in C^n \vert \vert z - a_{ii} \vert \leq {\sum}^n_{j=1 , j \ne i } \vert a_{ij} \vert \}$

$A \in C^{n \times n} ~~~A = ( a_{ij} )$

Example : $A = \left [ \matrix{ 1 & 2 & 3 \cr 4 & 5 & 6 \cr 7 & 8 & -9 \cr } \right ]$

Gershgorin Circles are :

$D_1 \equiv \{ z : \vert z-1 \vert \leq 6 \}$

$D_2 \equiv \{ z : \vert z-5 \vert \leq 10 \}$ $D_3 \equiv \{ z : \vert z+9 \vert \leq 15 \}$

[Thm] ( Gershgorin Thm )

If $A \in C^{n \times n}$ , then the eigenvalues of A contained the main union of the Gershgorin circles

$\lambda (A) \geq {\cup}_i D_i \equiv \{ z \in C^n \vert \vert z - a_{ii} \vert \leq {\sum}^n_{j=1, j \ne i } \vert a_{ij} \vert \vert \}$

Example : $A = \left [ \matrix{ 10 & 1 \cr 1 & 8 \cr } \right ]$

Note : $\lambda (A) = \{ 9 + \sqrt 2 , 9 - \sqrt 2 \}$

$\lambda \in \lambda (A)$ Let x be an Eigenvector ( $w , r , t , \lambda$)

s.t. ${\Vert x \Vert}_{\infty} = 1$ Let i be the index , s.t. x_i = 1

$\Rightarrow {(Ax)}_i = {\sum}^n_{j=1} a_{ij} x_j = {( \lambda x )}_i = \lambda ... ...vert a_{ij} \vert \vert x_j \vert = {\sum}^n_{j=1 , j \ne i} \vert a_{ij} \vert$

$A \rightarrow A + E$

[Thm] If A is diagonized by a similary transform P^-1 A P

and E be any matrix , then the eigenvalues of

A+E lies in the union of $\{ \lambda : \vert \lambda - {\lambda}_i \vert \leq k_{\infty} (P) {\Vert E \Vert}_{\infty} \}$

where ${\lambda}_i \in \lambda (A)$

Example : $A \sim D = \left [ \matrix{ 1 & 0 & 0 \cr 0 & 2 & 0 \cr 0 & 0 & 3 \cr } \right ]$ $\lambda (A) = \{ 1 , 2 , 3 \}$ If D = P^-1 A P , and A is perturbed to E , then if $\lambda \in \lambda (A + E)$

and $E = \left [ \matrix{ 0 & 0 & 0.2 \cr 0 & 0 & 0 \cr 0.1 & 0 & 0 \cr } \right ]$ $\vert \lambda - 1 \vert \geq \kappa (P) (0.2)$ ,  $\vert \lambda - 2 \vert \geq \kappa (P) (0.2)$ ,  $\vert \lambda - 3 \vert \geq \kappa (P) (0.2)$

<Proof> If D = P^-1 A P ,then $\lambda (A+E)$ = $\lambda (P^{-1} (A+E) P)$ = $\lambda ( P^{-1} A P + P^{-1} E P )$ = $\lambda ( 0 + P^{-1} E P )$ Let C = P^-1 E P , and D = ( d_ij )    C = ( c_ij ) then ( From the Gershgorin's Thm )

$\vert \lambda - {\lambda}_i - c_{ii} \vert$ $\leq$ ${\sum}^n_{j=1 j \ne i} \vert d_{ij} + c_{ij} \vert$ = ${\sum}^n_{ j=1 , j \ne i } \vert c_{ij} \vert$

$\vert \lambda - {\lambda}_i \vert$ $\leq$ $\vert \lambda - {\lambda}_i - c_{ij} \vert + \vert c_{ii} \vert$

$\leq$ $\vert c_{ii} + {\sum}^n_{j=1 , j \ne } \vert c_{ij} \vert$

= ${\sum}^n_{j=1} \vert c_{ij} \vert$ $\leq$ ${\Vert C \Vert}_{\infty}$

= ${\Vert P^{-1} E P \Vert }_{\infty}$ $\leq$ ${\Vert P^{-1} \Vert}_{\infty} {\Vert E \Vert}_{\infty} {\Vert P \Vert}_{\infty}$ = ${\kappa}_{\infty} (P) {\Vert E \Vert}_{\infty}$

If A is Hermitian ( i.e. A = A^* ) ( or Symmetric if $A \in {I\!\!R}^{n \times n}$ )

then A is unitary similary to a diagonal matrix D

i.e. $\exists v$ unitary ( orthogonal ) s.t. D = v^* A v

Note : ${\Vert v \Vert}_2 = 1$ ( or $\Vert u_j \Vert = 1 , u_j$ are column vectors )

$\Rightarrow$ ${\Vert v \Vert}_{\infty}$ $\leq$ $\sqrt n \Rightarrow {\kappa}_{\infty} (v) \leq n$

$\Rightarrow$ $\vert \lambda - {\lambda}_i \vert$ $\leq$ ${\kappa}_{\infty} (v) {\Vert E \Vert}_{\infty}$ $\leq$ $n {\Vert E \Vert}_{\infty}$

1. ${\Vert x \Vert}_{\infty}$ $\leq$ ${\Vert x \Vert}_2$ $\leq$ ${\Vert x \Vert}_1$2. ${\Vert x \Vert}_1$ $\leq$ $n {\Vert x \Vert}_{\infty}$ ${\Vert x \Vert}_2$ $\leq$ $\sqrt n {\Vert x \Vert}_{\infty}$

Exercise 4.2.2 : 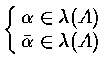$\left \{ \matrix{ \alpha \in \lambda (A) \cr \bar {\alpha} \in\lambda (A) \cr } \right$If $\alpha \in \lambda (A)$ and P(X) : char. poly. , then P(X) = 0 $\Rightarrow$ $P( \bar {\alpha} ) = 0$

Example :

P(X) = x³ + 3 x² + 3 x + 1

$P( \alpha ) = {\alpha}^3 + 3 {\alpha}^2 + 2 \alpha + 1$

$P( \bar {\alpha} ) =$ ${\bar {\alpha}}^3 + 3 {\bar {\alpha}}^2 + 2 {\bar {\alpha}} + 1$= $\overline {{\alpha}^3 + 3 {\alpha}^2 + 2 \alpha + 1 }$= $\overline { P ( \alpha ) }$ = 0

$\left \{ \matrix{ \overline { \alpha \beta } = \bar { \alpha } \cdot \bar { \be... ...r \overline { \alpha + \beta } = \bar { \alpha } + \bar { \beta } \cr }\right$

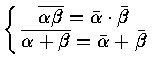
[Thm] Real Schur's Thm ( Schur's Thm v^* A v = T = D + N )

s.t. Q^* A Q = T = $\left [ \matrix{ T_{11} & T_{12} & \cdots & T_{1n} \cr & T_{22} & \cdots & \vdots \cr && \ddots & \vdots \cr 0 &&& T_{pp} \cr } \right ]$

where $T_{ii} \in {I\!\!R}^{ 1 \times 1 }$ or ${I\!\!R}^{ 2 \times 2 }$