[Def] A ![]() B ( similar ) if
B ( similar ) if ![]() P nonsingular s.t.
A =
P-1 B P ( where
P nonsingular s.t.
A =
P-1 B P ( where
![]() )
)
[Thm] Similar matrices have the same Eigenvalues
<Proof> If
![]() nonsingular s.t.
A = P-1 B P
Consider (
nonsingular s.t.
A = P-1 B P
Consider (
![]() ) =
) =
![]() =
=
![]() =
=
![]() =
=
![]() =
=
![]() =
=
![]()
[Thm] If v is an Eigenvector of A with associated Eigenvalues ![]()
If
B = P-1 A P , then
(P-1 V) is an Eigenvector of B with associated ![]()
<Proof>
![]() , and
B = P-1 A P
, and
B = P-1 A P
![]() P B P-1 v =
P B P-1 v =
![]() =
=
![]()
[Def]
![]() is simple if the
Eigenvectors of A form a basis for Cn
is simple if the
Eigenvectors of A form a basis for Cn
[Def]
1. Algebraic multiplicity :
if the characteristic polynomial of A is given by
f(x) =
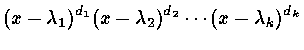
, then the order di is called the algebraic multiplicity of
![]() 2.
2.
![]() =
=
![]() , then the geometric multiplicity =
, then the geometric multiplicity =
![]()
Note : Geometric multiplicity ![]() Algebraic multiplicity
Algebraic multiplicity
Example :
![$A = \left [
\matrix{ 1 & 0 \cr
0 & 1 \cr
}
\right ]$](img24.gif) Rank =
Rank =
![$\left [
\matrix{ 0 & 0 \cr
0 & 0 \cr
}
\right ] = 0 $](img25.gif) Nullity =
Nullity =
![$\left [
\matrix{ 0 & 0 \cr
0 & 0 \cr
}
\right ] = 2 $](img26.gif)
Characteristic polynomial = ( x - 1 )2
(
![]() )
: Algebraic multiplicity = 2
: geometric multiplicity = 2
)
: Algebraic multiplicity = 2
: geometric multiplicity = 2
![$B = \left [
\matrix{ 0 & 1 \cr
0 & 0 \cr
}
\right ] $](img28.gif)
Characteristic polynomial = x2
: Algebraic multiplicity = 2
: geometric multiplicity = 1
[Thm] Similar Transformation preserve both the algebraic and geometric multiplicities
Companion matrix
![$A = \left [
\matrix{ 0 & 1 &&& \cr
& 0 & 1 && \cr
&& \ddots & \ddots & \cr
&&& 0 & 1 \cr
-a_0 & -a_1 & \cdots & \cdots & -a_{n-1} \cr
}
\right ]$](img29.gif) then
then
![]() =
=
![]() ( Jodan Form , Rational Form )
( Jodan Form , Rational Form )
[Thm] ( diagonalizable )
If
![]() is simple with l.I.
eigenvectors
is simple with l.I.
eigenvectors
![]()
then there exists
![]() where
ui are column vectors s.t.
D = u-1 A u
, where D =
where
ui are column vectors s.t.
D = u-1 A u
, where D =
![$\left [ \matrix{ {\lambda}_1 && 0 \cr & \ddots & \cr
0 && {\lambda}_n \cr } \right ]$](img34.gif)
( i.e. ![]() )
)
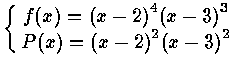
where f : characteristic poly. of A P : minimal poly. of A
Unitary Similary Transformation
A similar to B ( ![]() )
)
if ![]() nonsingular
nonsingular
s.t. A = P-1 B P
(
![]() )
)
[Def]
![]() is unitary if U U* = I ( i.e.
U* = U-1 )
is unitary if U U* = I ( i.e.
U* = U-1 )
where U* is the conjugate transpose of U
Note 1.: If U unitary and
![]() is orthogonal
is orthogonal
![$A = \left [
\matrix{ 1+i & 3 \cr
-2i & 1-i \cr
}
\right ] ~~~~
A^* = \left...
...ht ] =
\left [
\matrix{ 1-i & 2i \cr
3 & 1+i \cr
}
\right ]
\par\exists U$](img42.gif) unitary matrix , then A is unitary similary to B
unitary matrix , then A is unitary similary to B
( in
![]() is called orthogonal similary )
is called orthogonal similary )
[Def] A is Hermite , if
![]()
( in
![]() is called symmetric )
is called symmetric )
Note 2.: Unitary matrix have the same properties as the orthogonal matrix
Example :
(i.)
(vx , vy ) = ( x , y ) = y* x (ii.)
![]() (iii.) If
(iii.) If
![]() are unitary
are unitary
![]() also unitary
(iv.) A = VR ( the same to
also unitary
(iv.) A = VR ( the same to
![]() )
)
![]() the set of all eigenvalues
the set of all eigenvalues
If
![]() =
=
![]()
![]() det (A) =
det (A) =
![]() =
=
![]()
tr (A) =
![]()
![]() S is invariant ( of A ) , if
S is invariant ( of A ) , if
![]()
Note : x is eigenvector of A
![]()
(
![]() eigenspace of x is invariant ( of A ))
eigenspace of x is invariant ( of A ))
Note : If
![]() invariant
invariant
If
![]()
the same to
![]()
Ax = xB is called the Similary Transformation
( Note : If
![]() nonsingular
nonsingular
![]() )
)
[Lemma] If
![]() satisfy
satisfy
![]() , then
, then
![]() unitary s.t.
unitary s.t.
![$Q^* A Q = T = \left [
\matrix{ T_{11} & T_{12} \cr
0 & T_{22} \cr
}
\right ]$](img66.gif)
Note : 1.
![]() 2. This Q is the Q of analysis x = QR
2. This Q is the Q of analysis x = QR
Example :
![$\left [
\matrix{ 67 & 177.60 & -63.20 \cr
-20.40 & 95.88 & -87.16 \cr
22.80 & 67.84 & 12.12 \cr
}
\right ]$](img68.gif)
![$Q^T Q Q = T = \left [
\matrix{ 25 & -90 & 5 \cr
0 & 147 & -104 \cr
0 & 146 & 3 \cr
}
\right ]$](img69.gif)
<Proof>
![$x = QR = Q {\left [
\matrix{ R \cr 0 \cr }
\right ]}^P$](img70.gif) is the QR factorization of x
is the QR factorization of x
Because
![$Ax = xB \Rightarrow A Q \~ R = A \~ R B
\Rightarrow Q^* A Q \left [
\matrix...
...
\matrix{ R \cr 0 \cr }
\right ] =
\left [
\matrix{ R \cr 0 \cr }
\right ]$](img71.gif)
![]() ( because R is nonsingular )
( because R is nonsingular )
[Schur's Theorem]
If
![]() , then there exist Q unitray
s.t.
Q* A Q = T = D + N , where D =
, then there exist Q unitray
s.t.
Q* A Q = T = D + N , where D =
![$\left [ \matrix{ {\lambda}_1 && 0 \cr & \ddots \cr
0 && {\lambda}_n \cr } \right ]$](img73.gif)
![]() are eigenvalues of A
are eigenvalues of A
Moreover
![]() can be rearranged in any order
can be rearranged in any order
<Proof> (By Induction on n )
n = 1 ( get
![]() ) (
) (
![]() )
)
then from the Lemma ![]() , unitary
, unitary
s.t.
![$v^* A v = \left [
\matrix{ \lambda & w \cr
0 & c \cr
}
\right ]$](img77.gif) If the Thm is hold for all order
If the Thm is hold for all order ![]() n - 1
n - 1
![]() unitary s.t.
unitary s.t.
![]()
Let
![$Q = diag ( 1 , \~ Q ) = \left [
\matrix{ 1 & 0 \cr
0 & \~ Q \cr
}
\right ]$](img80.gif)
then Q* A Q =
![$\left [ \matrix{ \lambda & 0 \cr 0 & \~ T \cr } \right ]$](img81.gif) =
T = D + N =
=
T = D + N =
![$\left [ \matrix{ {\lambda}_1 && 0 \cr & \ddots \cr
0 && {\lambda}_n \cr } \right ]$](img73.gif)
Example :
![$A = \left [
\matrix{ 75 & 200 \cr
-50 & 75 \cr
}
\right ]$](img82.gif) then
then
![$Q = \left [
\matrix{ .8944i & .4472 \cr
-.4722 & -.8944 \cr
}
\right ]$](img83.gif)
Q* A Q = T =
![$\left [
\matrix{ 75+100i & -150 \cr
0 & 75-100i \cr
}
\right ]$](img84.gif) =
=
![$\left [
\matrix{ 75+100i & 0 \cr
0 & 75-100i \cr
}
\right ] +
\left [
\matrix{ 0 & -150 \cr
0 & 0 \cr
}
\right ]$](img85.gif)
Note : If A is nonsingular
![]() N = 0
N = 0
[Def]
![]()
![]() departure from nonsingularity
departure from nonsingularity
N is independent choice of Q
Note : Simple matrices are dense in
![]() ( or
( or
![]() )
( i.e. If A is choosen randomly
)
( i.e. If A is choosen randomly
![]() slmost all A are simple )
slmost all A are simple )
If
![]() are simple matrices
are simple matrices
![]() for any
for any
![]() s.t.
s.t.
![]()
[Def]
![]() is said to be normal if
A A* = A* A
is said to be normal if
A A* = A* A
[Thm] ( Spectral Thm for Normal Matrices )
![]() is normal
is normal
![]() unitary , s.t.
Q* A Q = D , D diagonal
unitary , s.t.
Q* A Q = D , D diagonal
<Proof> "
![]() "
Q* A Q = D
"
Q* A Q = D
D D* = (Q* A Q)(Q* A Q)* = Q* A A* Q
![]() =
Q D D* Q* = A A*
=
Q D D* Q* = A A*
and
![]()
![]()
"
![]() " A is normal
" A is normal
![]() T is normal
T is normal
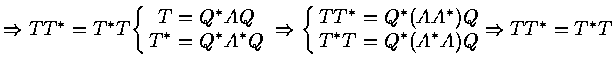
![]()
s called departure from the normality
A is normal if A A* = A* A
[Thm] A is normal
![]() unitary s.t.
v* A v = D
unitary s.t.
v* A v = D
Note :
1.
![]() ( Schur's Decomposition )
2.
( Schur's Decomposition )
2.
![]()
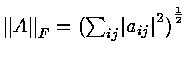
Example :
![$A = \left [
\matrix{ 1 & 2 \cr
3 & 4 \cr
}
\right ] ~~~~
{\Vert A \Vert}_F = \sqrt {1+4+9+16} $](img103.gif)
Note : Simple matrices are dense in
![]() .
.
For all
![]() is simple
is simple
![]()
Note : Matrices norm are equivalent , i.e.
![]() are two matrices norm
are two matrices norm
![]() s.t.
s.t.
![]()
Note :
![]() is indep. of choice of Q .
Q A Q = D + N
is indep. of choice of Q .
Q A Q = D + N
Example :
![$\overbrace {A \sim T}^{~unitary~similary} = \left [
\matrix{ 2 & 4 & 5 \cr
0 ...
... +
\left [
\matrix{ 0 & 4 & 5 \cr
0 & 0 & 6 \cr
0 & 0 & 0 \cr
}
\right ] $](img110.gif)
![$A \sim T_1 = \left [
\matrix{ 2 & 1 & 0 \cr
0 & 2 & 0 \cr
0 & 0 & 3 \cr
}
\right ] $](img111.gif) ( Jordan Form of A )
( Jordan Form of A )
Nonunitary Transformation
If
![]() , A =
, A =
![$\left [\matrix{ T_{11} & T_{12} \cr 0 & T_{22} \cr } \right ]$](img112.gif) p + q = n
p + q = n
[Def]
![]()
![]()
![]() s.t.
s.t.
![]() , then
, then ![]() is nonsingular
is nonsingular
![]()
![]()
If ![]() is nonsingular and Y is defined by
is nonsingular and Y is defined by
![$Y = \left [ \matrix{ I_p & z \cr 0 & I_q \cr } \right ]$](img119.gif)
![]() , then
Y-1 A Y =
, then
Y-1 A Y =
![$\left [ \matrix{ T_{11} & 0 \cr 0 & T_{12} \cr }\right ]$](img121.gif)
[Thm] If A =
![$\left [ \matrix{ T_{11} & T_{12} & \cdots & T_{1n} \cr
0 & T_{22} && \vdots \cr \vdots && \ddots & \vdots \cr
0 & \cdots & \cdots & T_{nn} \cr } \right ]$](img122.gif) ,
,
![]() Y s.t. (YQ)-1 A (YQ)=
Y s.t. (YQ)-1 A (YQ)=
![$\left [\matrix{ T_{11} &&& 0 \cr & T_{22} && \cr
&& \ddots & \cr 0 &&& T_{nn} \cr } \right ]$](img123.gif)
where Tii are square and
![]() =
=
![]() for all
for all ![]()
[Cor] If
![]() , then
, then ![]() x nonsingular s.t.
x-1 A x =
x nonsingular s.t.
x-1 A x =
![]()
where all
![]() are distinct
are distinct
![]()
the integer
![]()
Note : ni is the algebraic multipicity of
![]()
If
![]() , then
Range(xi) are invariant subspace
, then
Range(xi) are invariant subspace
![]()
![]()
Jordan's Block : Ji =
![$\left [
\matrix{ {\lambda}_1 & 1 &&&& 0 \cr
& \ddots & \ddots &&& \cr
&& {\l...
...ddots & \ddots & \cr
&&&& \ddots & 1 \cr
0 &&&&& {\lambda}_1 \cr
}
\right ]$](img131.gif)
![]() =
=
![$\left [
\matrix{ {\lambda}_1 & \ddots & * & * & * \cr
& {\lambda}_1 & \ddots...
...s & \ddots & * \cr
&&& \ddots & \ddots \cr
0 &&&& {\lambda}_1 \cr
}\right ]$](img133.gif) Note : Transformation is called "nonunitary transformation" .
Note : Transformation is called "nonunitary transformation" .
Example :
![]() ,
f(x) =
( t - 2 )4 ( t - 3 )3 ,
P(x) =
( t - 2 )2 ( t - 3 )3
,
f(x) =
( t - 2 )4 ( t - 3 )3 ,
P(x) =
( t - 2 )2 ( t - 3 )3
Jordan Form :
J1 =
![$\left [ \matrix{ 2 & 1 &&&&& \cr 0 & 2 &&&& 0 & \cr
&& 2 & 1 &&& \cr && 1 & 2 &&& \cr &&&& 3 & 1 & \cr
& 0 &&& 0 & 3 & \cr &&&&&& 3 \cr } \right ]$](img135.gif)
J2 =
![$\left [ \matrix{ 2 & 1 &&&&& \cr 0 & 2 &&&&& \cr
&& 2 &&&& \cr &&& 2 &&& \cr &&&& 3 & 1 & \cr
&&&& 0 & 3 & \cr &&&&&& 3 \cr } \right ]$](img136.gif)
the eigenspace of
![]()
the eigenspace of
![]()
Localized Eigenvalues and Derturbation
Gershgorin Circles :
Di =
![]()
![]()
Example :
![$ A = \left [
\matrix{ 1 & 2 & 3 \cr
4 & 5 & 6 \cr
7 & 8 & -9 \cr
}
\right ]$](img141.gif)
Gershgorin Circles are :
![]()
![]()
![]()
[Thm] ( Gershgorin Thm )
If
![]() , then the eigenvalues of A contained
the main union of the Gershgorin circles
, then the eigenvalues of A contained
the main union of the Gershgorin circles
![]()
Example :
![$A = \left [
\matrix{ 10 & 1 \cr
1 & 8 \cr
}
\right ]$](img146.gif)
Note :
![]()
![]() Let x be an Eigenvector (
Let x be an Eigenvector (
![]() )
)
s.t.
![]() Let i be the index , s.t. xi = 1
Let i be the index , s.t. xi = 1
![]()
![]()
[Thm] If A is diagonized by a similary transform P-1 A P
and E be any matrix , then the eigenvalues of
A+E lies in the union of
![]()
where
![]()
Example :
![$A \sim D = \left [
\matrix{ 1 & 0 & 0 \cr
0 & 2 & 0 \cr
0 & 0 & 3 \cr
}
\right ]$](img155.gif)
![]() If
D = P-1 A P ,
and A is perturbed to E , then if
If
D = P-1 A P ,
and A is perturbed to E , then if
![]()
and
![$E = \left [
\matrix{ 0 & 0 & 0.2 \cr
0 & 0 & 0 \cr
0.1 & 0 & 0 \cr } \right ]$](img158.gif)
![]() ,
,
![]() ,
,
![]()
<Proof> If
D = P-1 A P
,then
![]() =
=
![]() =
=
![]() =
=
![]() Let
C = P-1 E P , and
D = ( dij ) C = ( cij )
then ( From the Gershgorin's Thm )
Let
C = P-1 E P , and
D = ( dij ) C = ( cij )
then ( From the Gershgorin's Thm )
![]()
![]()
![]() =
=
![]()
![]()
![]()
![]()
![]()
![]()
=
![]()
![]()
![]()
=
![]()
![]()
![]() =
=
![]()
If A is Hermitian ( i.e.
A = A* ) ( or Symmetric if
![]() )
)
then A is unitary similary to a diagonal matrix D
i.e. ![]() unitary ( orthogonal ) s.t.
D = v* A v
unitary ( orthogonal ) s.t.
D = v* A v
Note :
![]() ( or
( or
![]() are column vectors )
are column vectors )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
1.
![]()
![]()
![]()
![]()
![]() 2.
2.
![]()
![]()
![]()
![]()
![]()
![]()
Exercise 4.2.2 :
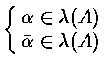 If
If
![]() and P(X) : char. poly. ,
then P(X) = 0
and P(X) : char. poly. ,
then P(X) = 0
![]()
![]()
Example :
P(X) = x3 + 3 x2 + 3 x + 1
![]()
![]()
![]() =
=
![]() =
=
![]() = 0
= 0
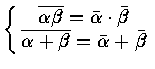
[Thm] Real Schur's Thm ( Schur's Thm v* A v = T = D + N )
s.t.
Q* A Q = T
=
![$\left [ \matrix{ T_{11} & T_{12} & \cdots & T_{1n} \cr
& T_{22} & \cdots & \vdots \cr && \ddots & \vdots \cr
0 &&& T_{pp} \cr } \right ]$](img198.gif)
where
![]() or
or
![]()