[Def]
![]() If
If
![]() , then v is called the eigenvector
of A associated with the Eigenvalue
, then v is called the eigenvector
of A associated with the Eigenvalue ![]() .
.
![]() is a subspace of
is a subspace of
![]() is called the Eigen Space
of A associated with
is called the Eigen Space
of A associated with ![]()
< Characteristic Polynomial :
![]() >
>
If ![]() is an eigenvalue of A , then
is an eigenvalue of A , then
1.
![]() 2.
2.
![]() is singular
is singular
![]() If
If ![]() is an eigenvalue
is an eigenvalue
![]()
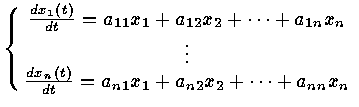
![]()
The solution is of the form x(t) = f(t) v
![]() differentiate with respected to t .
differentiate with respected to t .
![]()
because
f' (t) v = A f(t) v
![]()
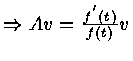
Let
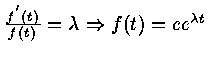
![]()
1. Power Method ( Find MAX. eigenvalue ) 2. Inverse Power Method ( Find MIN. eigenvalue) 3. Shift Inverse Power Method ( Find the eigenvalue close to fixed u )
Power Method :
If
![]() are
eigenvalue of A with
are
eigenvalue of A with
![]() and
and
![]() are eigenvectors and linear indep.
associated with
are eigenvectors and linear indep.
associated with
![]() respectively .
respectively .
STEP : Let q be any vector in
![]() consider the sequence
consider the sequence
![]()
because
![]() form a basis of
form a basis of
![]()
![]()
W.l.o.G. ( Without loss of Generality )
We may assume
![]()
![]()
![]() =
=
![]()
![]() A2 q =
A2 q =
![]()
In general ,
An q =
![]() =
=
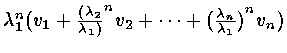
![]()
![]() =
=
![]() +
+
![]() +
+
![]()
=
![]()
An q =
![]() where
where
![]() when
when
![]()
Let ![]() be a linear functional [ for example :
be a linear functional [ for example :
![]() ]
]
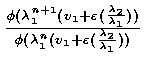 =
=
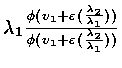 =
=
![]()
Example : 4.3.5
A =
![$\left [ \matrix{ 9 & 1 \cr 1 & 2 \cr } \right ]$](img43.gif) ,
q0 =
,
q0 =
![${\left [ \matrix{ 1 & 1 \cr } \right ]}^T$](img44.gif)
[Sol]
STEP 1. Find a sequence
![]() A q0 =
A q0 =
![$\left [ \matrix{ 9 & 1 \cr 1 & 2 \cr } \right ]$](img43.gif)
![]() =
=
![$\left [ \matrix{ 10 \cr 3 \cr } \right ]$](img47.gif) = q1
= q1
STEP 2. ![]() =
=
![]()
![]()
![${\left \Vert \matrix{
\left [ \matrix{ 10 \cr 3 \cr } \right ] \cr } \right \Vert }_{\infty}$](img49.gif) = 10 =
= 10 =
![]()
![]()
![]() =
=
![]()
![$\left [ \matrix{ 10 \cr 3 \cr } \right ]$](img47.gif) =
=
![$\left [ \matrix{ 1 \cr { 3 \over {10} } \cr } \right ]$](img53.gif)
STEP 3. repeat STEP 2.
A2 q0
![]() A (A q0) = A q2 =
A (A q0) = A q2 =
![]()
consider
![]() =
=
![$\left [ \matrix{ 9 & 1 \cr 1 & 2 \cr } \right ]$](img43.gif)
![$\left [ \matrix{ 1 \cr { 3 \over {10} } \cr } \right ]$](img53.gif) =
=
![$\left [ \matrix{ 9.3 \cr 1.6 \cr } \right ]$](img56.gif) = q2
= q2
![]() =
=
![]() =
=
![$\left [ \matrix{ 1 \cr {{1.6} \over {9.3}} } \right ]$](img59.gif)
By Table 4.1 ( P213 )
Eigenvalue : 9.140055
Eigenvector : ( 1 , 0.140055 )
![]() =
=
![]()
![]() An q0 =
An q0 =
![]()
![]() , when
, when
![]()
![]()
![]()
![]()
![]() =
=
![]() =
=
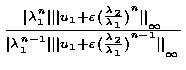
![]()
[Thm] If a is nonsingular , if ![]() is an Eigenvalue of A ,
then
is an Eigenvalue of A ,
then
![]() isi an Eigenvalue of A-1 .
isi an Eigenvalue of A-1 .
<Proof> If ![]() is an Eigenvalue of A
is an Eigenvalue of A
![]()
Inverse Power Method :
( For finding the smallest Eigenvlaue of A )
1. If
![]() 2. and
2. and
![]() are L.I. Eigenvectors .
3. A is nonsingular .
are L.I. Eigenvectors .
3. A is nonsingular .
![]()
apply Power Method to A-1
![]()
![]() can be found by regular Power Method on A-1
can be found by regular Power Method on A-1
Shift Inverse Power Method :
[Thm] If ![]() is an Eigenvalue of A , then
is an Eigenvalue of A , then
![]() is an Eigenvalue of (A - uI) .
is an Eigenvalue of (A - uI) .
<Proof> because
![]()
![]()
so
![]() is an Eigenvalue of
( A - uI )
is an Eigenvalue of
( A - uI )
1. Given
![]()
s.t.
![]() , and
, and
![]() for all
for all ![]() 2.
2.
![]() L.I. Eigenvectors
3. A-1 exists
L.I. Eigenvectors
3. A-1 exists
Example :
![]() are Eigenvalue of A
are Eigenvalue of A
[Sol] Let u = 1.2 , consider
![]() are Eigenvalues of
( A - uI )
are Eigenvalues of
( A - uI )
1. If
![]() are Eigenvalues of A ,
are Eigenvalues of A ,
then
![]() are Eigenvalues of A - uI2. If
are Eigenvalues of A - uI2. If
![]() are the smallest Eigenvalue of A - uI ,
are the smallest Eigenvalue of A - uI ,
then Apply the inverse Power Method on (A - uI) ,
we can find
![]() (
(
![]() can be fonud )
can be fonud )
Issue :
1. Power Method : find MAX. Eigenvalue and Eigenvector 2. Inverse Power Method : find MIN. Eigenvalue and Eigenvector 3. Shift Inverse Power Method : find the Eigenvalue colse to fixed u