![]() , and
, and
![]()
then
![]()
A ej : the j-th column of A
(eiT A : the i-th row of A )
![]()
![]()
[Def]
![]() ,
,
![]() is called isometric
is called isometric
![]()
(
![]() )
)
i.e. the column vectors are O.N.
![]() ,
then
,
then
![]() where
where
![]()
![]() and
and ![]() is isometric .
is isometric .
<Proof>
A = QR , Q
![]() ,
,
![]()
![]() where
where
![]() ,
R =
,
R =
![]()
![]()
![]()
![]() =
=
![]() =
=
![]()
Gram-Schmidt
![]() : O.N.vectors
: O.N.vectors
Exercise : P168 Ex3.4.1 Ex3.4.3
Gram-Schmidt process
![]() is a basis
is a basis
![]() orthonormal basis
orthonormal basis
such procsee is called Gram-Schmidt orthonomalization .
![]()
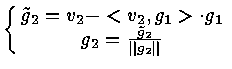
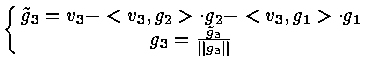
In general
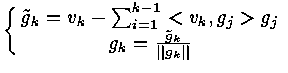
![]()
![]() ,
,
Let
![]()
Let rjk = < vk , gj > , j < k
![]() =
=
![]()
![$\left [ \matrix{ r_{11}& r_{12} & \cdots & r_{1n} \cr
0 & r_{22} & \cdots & r_{2n} \cr 0 & 0 & \ddots & \vdots \cr
0 & 0 & 0 & r_{nn} \cr } \right ] $](img35.gif)
vi are the column vextors of V
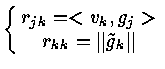
1. Subspace :
![]() is subspace of
is subspace of
![]()
if
![]() and
and
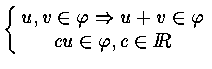
2. Linear Independent
3. Span
![]() =
=
![]()
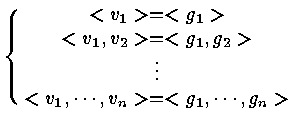
If
![]() =
=
![]()
![]() =
=
![]()
![]() subspace of
subspace of
![]()
![]() is the orthogonal complement of
is the orthogonal complement of ![]() .
.
Note :
1.
![]() is also a subspace of
is also a subspace of
![]() .
2.
.
2.
![]()
![]() are the O.N. vectors .
are the O.N. vectors .
[Thm]
![]() subspace of
subspace of
![]() ,
then
,
then
![]()
( i.e.
![]() if
if
![]() , then
, then
![]() ,where
,where
![]()
moreever ,
![]() )
)
<Proof>
![]()
![]() =
=
![]() =
=
![]()
and
![]() =
=
![]()
![]() =
=
![]() =
=
![]()
![]()
![]()
![]()
N(A) = null space of
![]()
R(A) = range of
![]() [Thm]
[Thm]
![]() then
< nx , y > = < x , AT y >
then
< nx , y > = < x , AT y >
![]() yT A x = (AT y)T x
yT A x = (AT y)T x
[Thm]
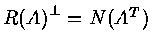
[Thm]
![]()
![]()
[Thm] If A is symmetric ,
![]()
![]()
![]()
If
![]() ( i.e.
( i.e.
![]() )
)
Range : R(A) =
![]()
Null space : N(A) =
![]()
<Proof of
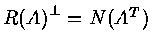 >
>
![]() If
If
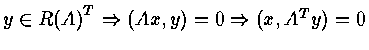 for all x
for all x
![]()
In particular
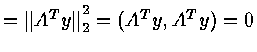
i.e.
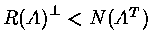
![]() If
If
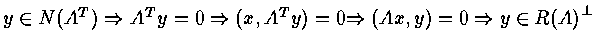
i.e.
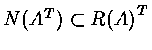
[Lemma]
![]()
[Thm]
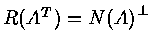
<Proof> Because
![$R {(A)}^{\bot} = N( A^T )
\par\Rightarrow R{( A^T )}^{\bot} = N( A^{TT} ) = N(A)
\par\Rightarrow {[ R{( A^T )}^{\bot} ]}^{\bot} = {[ N(A) ]^{\bot}} $](img91.gif)
![]()
Note : nullity (T) + range (T) = dim S
( If T : S
![]() S linear transformation )
S linear transformation )
Exercise : 3.5.7
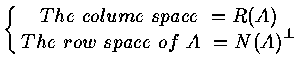
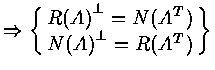 ( because column space A = row space of AT )
( because column space A = row space of AT )
![]() The Discrete Least-Square Problem
The Discrete Least-Square Problem
If
![]()
![]()
[Thm] ( Pythagorean Thm. )
![]() if
( u ,v ) = 0
if
( u ,v ) = 0
<Proof>
![]() =
< u , u > + < u , v > + < v , u > + < v , v >
=
=
< u , u > + < u , v > + < v , u > + < v , v >
=
![]()
Note : The Least-Square Error
![]()
[Thm] If
![]() ,
then
,
then
![]()
such that
![]()
where y is the unique element in ![]()
such that
![]()
( i.e. y is the orthogonal projection of b into ![]() )
)
[Cor] Let
![]() .
Then
.
Then
![]() =
=
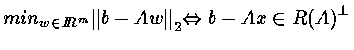
<Proof>
![]()
b = y + z , where
![]()
![]()
![]()
b = y + z uniquelly , with
![]() and
and
![]()
If
![]() s.t.
s.t.
![]()
![]()
consider
b - s = ( b - y ) + ( y - s ) ,
where
![]()
![]()
![]() =
=
![]()
![]()
![]() is
is
![]()
i.e.
![]()
![]()
![]()
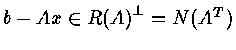
![]() AT ( b - Ax ) = 0
AT ( b - Ax ) = 0
![]() AT A x = AT b ( normal equation )
AT A x = AT b ( normal equation )
Note :
![]()
Note : 1. Solving L.S. Problems Ax = b ,
![]() is the same to solving normal equation
AT A x = AT b .
2. AT A
i. symmetry .
ii. nonneqative defined ( Positive semidefined
is the same to solving normal equation
AT A x = AT b .
2. AT A
i. symmetry .
ii. nonneqative defined ( Positive semidefined
![]() ).
3. If A is full rank ( i.e. rank A = m ) ,
then AT A is positive define
).
3. If A is full rank ( i.e. rank A = m ) ,
then AT A is positive define
![]() Chelosky Decomposition ( on AT A )
to solve the
( AT A ) x = AT b
Chelosky Decomposition ( on AT A )
to solve the
( AT A ) x = AT b
The way of solving Least Square Solution :
1. QR
2. Cholesky
3, A
![]() b
b
1. (AT A)T = AT ATT = AT A2. nonnegative defined
![]()
![]() 3. <Proof> A is full rank ,
AT A is nonsingular . If
3. <Proof> A is full rank ,
AT A is nonsingular . If
![]() for all
for all
![]()
![]() The Continuous Least Square Problem
The Continuous Least Square Problem
Discrete
![]()
Continuous
![]()
![]()
Inner Product :
![]()
![]()
2-norm
![]()
![]()
![]()
![]()
![]()
If
![]() are basis of
are basis of ![]() .
.
![]() ,
,
![]()
![]() ,
,
![]()
( m equations )
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
cx = d
c =
![$\left [ \matrix{ < {\phi}_1 , {\phi}_1 > , < {\phi}_2 , {\phi}_1 > ,
\cdots , <...
...> , < {\phi}_2 , {\phi}_m > , \cdots ,
< {\phi}_m , {\phi}_m > \cr } \right ] $](img151.gif)
![$\left [
\matrix{ c_1 \cr c_2 \cr \vdots \cr c_m \cr }
\right ] =
\left [
\matrix{ < f , {\phi}_1 > \cr
\vdots \cr
< f , {\phi}_m > \cr
}
\right ]$](img152.gif)
Note : c is 1. Symmetry . 2. Positive defined .