[Def] Q is orthogonal matrix if QQT = I
(
![]() QT = Q-1)
QT = Q-1)
Note : If Q orthogonal
![]() < gi , gj > =
< gi , gj > =
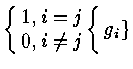 are row ( column ) vectors of Q .
are row ( column ) vectors of Q .
![]() is a inner product if
is a inner product if
1.
< x , y > = < y , x >
2. < ![]() x +
x + ![]() y , z > =
y , z > =
![]() < x , z > +
< x , z > + ![]() < y , z >
< y , z >
3.
![]() =
=
![]() < x . y > +
< x . y > + ![]() < x , z >
< x , z >
4. < x , x > ![]() 0 (
< x , x > = 0
0 (
< x , x > = 0
![]() < x = 0 >
< x = 0 >
Example : < x , y > = xT y = yT x
![]() = < x , x > = xT x
( because If
x = < x1 , x2 , ... , xn >
= < x , x > = xT x
( because If
x = < x1 , x2 , ... , xn >
![]()
![]() = x21 + x22 + ... , x2n )
= x21 + x22 + ... , x2n )
Cauchy Schwartz Inequality :
![]()
![]()
![]()
(
![]()
![]()
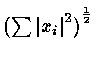
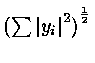 )
)
The angle of two vector x,y satisfy
![]() =
=
![]()
i.e. ![]() =
=
![]()
Least-Square Problems :
Example :
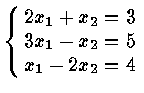
over-determinate
Least Square Problem :
Find the best answer xT , satisfy ![]() b - A xT
b - A xT ![]() minimal .
minimal .
Note : use A=QR can solve Least Square Solution xT of Ax=b .
[Thm]
![]()
![]() A=QR
A=QR
![]()
![]()
where Q : Orthogonal R : upper triangular
Use A = QR to solve the system of AX = b :
STEP 1. QRx = b
STEP 2. Rx = QTb
STEP 3.
Let QT b = d
STEP 4. Solve Rx = d by the backward subsitution.
In MATLAB , A = QR
>> [ Q , R ] = qr(A)
![$\left \{
\matrix{ Rotator \cr Reflector \cr } \right ~~~~~
\left [ \matrix{ \cos \theta & -\sin \theta \cr
\sin \theta & \cos \theta \cr } \right ]$](img26.gif) :
Rotator is an orthogonal matrix
:
Rotator is an orthogonal matrix
Q orthogonal
![]()
![]() =
=
![]()
[Lemma]
< Qx , Qy > = < x , y >
< Qx , Qy > = (Qy)T (Qx) = yT ( QT Q ) x = yT x = < x , y >
when x=y
![]() < Qx , Qy > = < x , x >
< Qx , Qy > = < x , x >
![]()
![]() Qx
Qx ![]() 22
22
![]()
Least-Square Problem :
![]()
![]()
![]()
![]() =
=
![]()
![]()
![]()
![]() =
=
![]()
![]()
![]()
![]() ( If A=QR )
( If A=QR )
A is nonsingular
![]() column vectors are l.I. .
column vectors are l.I. .
![]() row vectors are l.I. .
row vectors are l.I. .
Rotator :
Q =
![$\left [ \matrix{ \cos \theta & -\sin \theta \cr
\sin \theta & \cos \theta \cr } \right ]$](img34.gif)
(Q-1 = ) = QT =
![$\left [ \matrix{ \cos \theta & \sin \theta \cr
-\sin \theta & \cos \theta \cr } \right ] $](img35.gif)
![$\left [ \matrix{ x_1 \cr x_2 \cr } \right ]$](img36.gif) =
=
![]()
then , cos ![]() = ? , sin
= ? , sin ![]() = ?
= ?
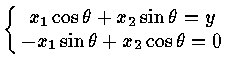
![]() x1 sin
x1 sin ![]() = x2 cos
= x2 cos ![]()
cos ![]() =
=
![]() ,
sin
,
sin ![]() =
=
![]()
( because must be satisfy ![]()
![]() +
+ ![]()
![]() = 1 )
Given matrix :
= 1 )
Given matrix :
![$ \left [
\matrix{ 1 &&&&&& \cr
& \ddots &&&&& \cr
&& C && -S && \cr
&&& \ddots &&& \cr
&& S && C && \cr
&&&&& \ddots & \cr
&&&&&& 1 \cr
}
\right ]$](img44.gif)
![$ \left [
\matrix{ x_1 \cr \vdots \cr x_i \cr \vdots \cr x_j \cr \vdots \cr x_n \cr }
\right ]$](img45.gif) =
=
![$\left [
\matrix{ x_1 \cr \vdots \cr \sqrt 5 \cr \vdots \cr 0 \cr \vdots \cr x_n \cr}
\right ]$](img46.gif)
![]()
i th j th column
C =
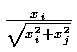 S =
S =
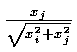
Reflectors : (Picture:)
Reflectors : Q
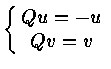
If P = u uT
![]() = 1 P2 = P ( projection )
= 1 P2 = P ( projection )
1. Pu = -u ![]()
because
Pu = u uT u = u
2. Pv = v ![]()
Pv = u ( ut v ) = 0
Let Q = I - 2P Q2 = I ( idempotent )
then , Qu = I(u) - 2P(u) = u - 2u = -u and QV = I(v) - 2P(v) = v - 0 = v
so satisfy Reflector i.e. Q = I - 2 u uT ( Householder transformation )
Note : u uT is the rank 1 matrix .
Q = I - r u uT , u has no limitation
![]() = 1 r =
= 1 r =
![]()
[Thm]
![]() =
=
![]() ,
, ![]() ! Q orthogonal s.t. Qx = y .
! Q orthogonal s.t. Qx = y .
Example : A =
![$\left [ \matrix{ 1 & 2 \cr 2 & 3 } \right ]$](img56.gif) = QR
= QR
We hope to find
QT , x , QT . A = R (
![]() A=QR )
A=QR )
Q
![]() =
=
![$\left [ \matrix{ \sqrt 2 \cr 0 \cr } \right ]$](img58.gif)
P147 Figure 3.4
1. x =
![]() +
+
![]()
[ Note :
![]() ]
]
2.
Q = I - r u uT , r =
![]()
u1 = ( x - y )
[ In the analysis of QR . x : the column vector of the origin A . y :
the column vector of the origin R ]
reduction u =
![]()
Q = I - 2 u uT
x - y =
![$\left [ \matrix{ 1 \cr 1 \cr } \right ] -
\left [
\matrix{ \sqrt 2 \cr 0 \cr }
\right ] =
\left [
\matrix{ 1 - \sqrt 2 \cr 1 \cr }
\right ] $](img63.gif)
so u =
![]()
![$\left [ \matrix{ 1 - \sqrt 2 \cr 1 \cr } \right ]$](img65.gif) ,
,
![$\left [ \matrix{ 1 - \sqrt 2 \cr 1 \cr } \right ]$](img65.gif)
![]() =
=
![$\left [ \matrix{ 3 - 2 \sqrt 2 & 1 - \sqrt 2 \cr
1 - \sqrt 2 & 1 \cr } \right ]$](img67.gif)
Q =
![$\left [ \matrix{ 1 & 0 \cr 0 & 1 \cr } \right ]$](img68.gif) -
-
![]()
![$\left [ \matrix{ 3 - 2 \sqrt 2 & 1 - \sqrt 2 \cr
1 - \sqrt 2 & 1 \cr } \right ]$](img67.gif)
Example :
A =
![$\left [ \matrix{ 1 & 2 & 3 \cr 2 & 3 & 4 \cr 2 & 1 & 3 \cr } \right ]$](img70.gif) = QR
= QR
Q = I - 2
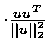 =
=
![$\left [ \matrix{ 1 & 0 & 0 \cr 0 & 1 & 0 \cr 0 & 0 & 1 \cr } \right ]$](img72.gif) -
-
![]()
![$\left [ \matrix{ 4 & -4 & -4 \cr -4 & 4 & 4 \cr -4 & 4 & 4 \cr } \right ]$](img74.gif)
=
![$\left [ \matrix{ 1 \over 3 & 2 \over 3 & 2 \over 3 \cr 2 \over 3 &
1 \over 3 & -3 \over 3 \cr 2 \over 3 & -2 \over 3 & 1 \over 3 \cr }
\right ]$](img75.gif) =
=
![${1 \over 3} \left [ \matrix{ 1 & 2 & 2 \cr 2 & 1 & -2 \cr
2 & -2 & 1 \cr } \right ]$](img76.gif)
QT . A =
![$\left [ \matrix{ 3 & {10} \over 3 & {17} \over 3 \cr
0 & 5 \over 3 & 4 \over 3 \cr 0 & - 1 \over 3 & 1 \over 3 \cr } \right ]$](img77.gif) =
=
![]()
![$\underbrace {
\left [ \matrix{ 1 & 2 & 2 \cr 2 & 1 & -2 \cr 2 & -2 & 1 \cr } \right ] }_{Q^T}$](img79.gif)
![$\left [ \matrix{ 1 & 2 & 3 \cr 2 & 3 & 4 \cr 2 & 1 & 3 \cr } \right ]$](img70.gif)
u = x - y =
![]() -
-
![]() =
=
![$\left [ \matrix{ -2 \cr 2 \cr 2 \cr} \right ]$](img82.gif)
![$\left [ \matrix{ -2 \cr 2 \cr 2 \cr} \right ]$](img82.gif)
![]() =
=
![$\left [ \matrix{ 4 & -4 & -4 \cr -4 & 4 & 4 \cr -4 & 4 & 4 \cr } \right ]$](img74.gif)
A = QR
1. Use Rotator ( Jacobi matrix )
Q =
![$\left [ \matrix{ \cos \theta & -\sin \theta \cr
\sin \theta & \cos \theta \cr } \right ]$](img34.gif)
2. Reflector :
Q = I - 2 u uT ( Orthogonal projector )
3. Gram-Schmidt Orthonomalization