空間中給定兩直線L1,L2,若P1是L1上的動點P2是L2上的動點,則       的最小值稱為直線 

                    L1 與 L2 的距離,此距離根據兩直線在空間中的情況可分為三種:

                     1. 重合或相交 :當兩直線重合或相交時,兩直線的距離為0.

                     2. 平行 : 兩直線平行時,兩線的距離,就是其中一線上任一點到另一直線的距離.

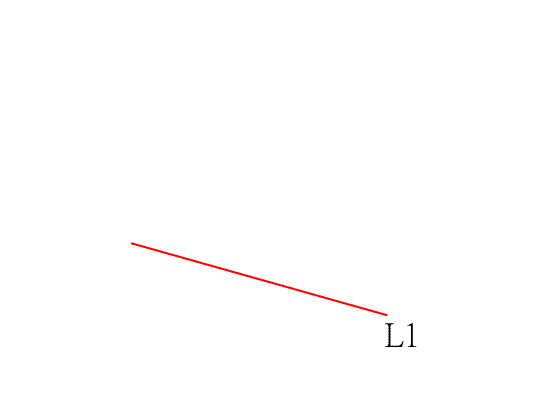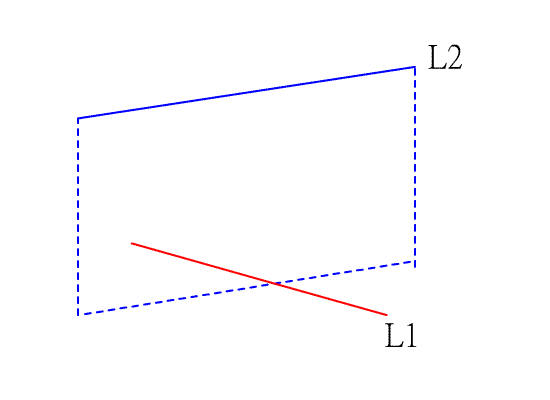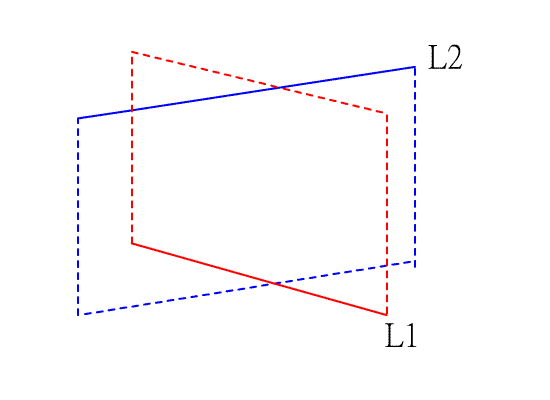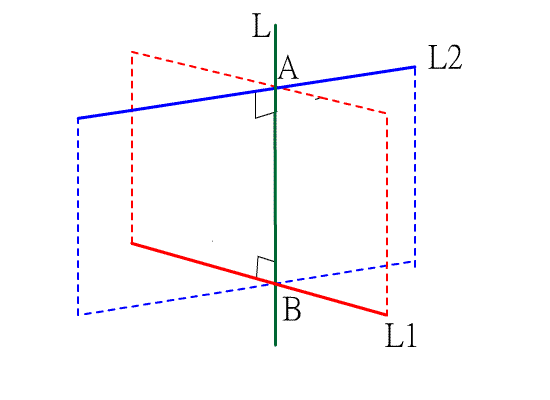
                     3. 歪斜 : L1與 L2 有一公垂線L,設 L 與 L1交於A,L 與 L2交於B,則P1,P2分別是L1,L2上的動點時,

                                     必有                .即     之長就是此組歪斜線的距離.如下圖:

                                           

　

                             <證明>

                                           

                                                     

                                                      

                                                      

                                                      因此       之長即歪斜線的距離.

　

       [上一頁]