過一點A作直線L的垂線,設垂足為B,則      之長就是點A到直線L的距離;換句話說,一點到一

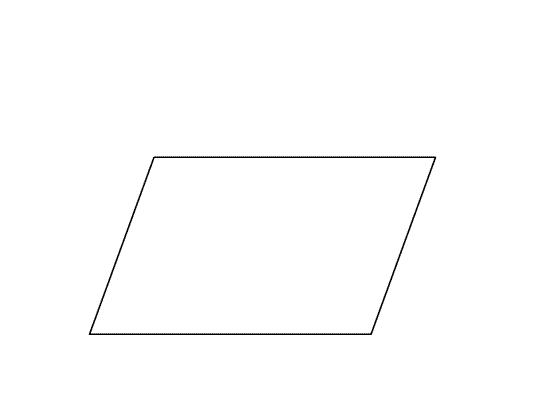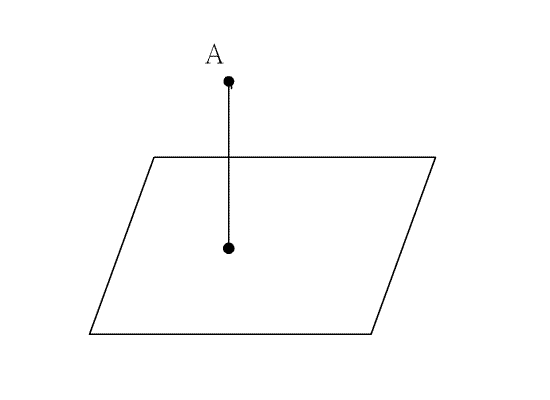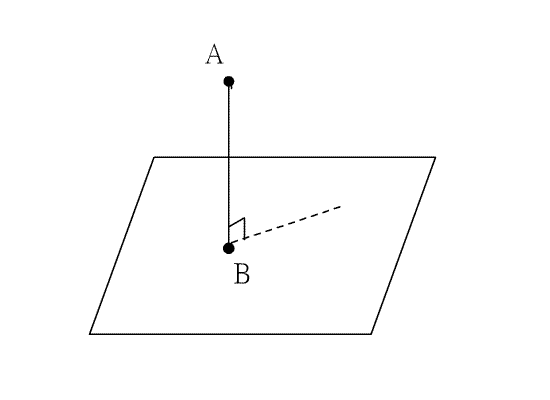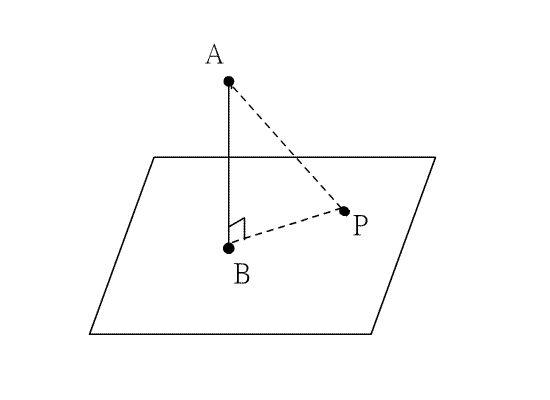
              直線的距離,就是此點與它在該直線上投影點的距離.考慮在空間坐標系中,假設A是一個定點,P是

              定平面E上的一個動點,則       的最小值就稱為點A到平面E的距離,由於直角三角形中,斜邊大於股

              長,所以點A到平面E的距離就是點A與它在平面E上投影點的距離.如下圖.

　

                                       

　

                 點到平面的距離計算方法:

                         

                         

                          即       ( x1 - x0, y1 - y0, z1 - z0 ) = t ( a, b, c) = ( ta, tb, tc )

                          亦即 ( x1, y1, z1 ) = ( x0 + at , y0 + bt, z0 + ct ),因為點B在平面E上,

                          所以 a( x0 + at ) + b( y0 + bt ) + c( y0 + bt ) + d = 0,

                          可得 

                                                         

                                                    

                                                                

                                                              =   

　

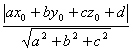
                                    因此點( x0, y0, z0 )到平面 ax + by + cz + d= 0 的距離為

                                                             .

　

　

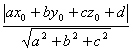[上一頁]