平面的點向式

                      當直線L與平面E垂直時,直線L的一個方向向量就稱為平面E的一個法向量,而且此法向量與

              平面上的任意一向量   都垂直;另一方面,若         ,且    與平面E上兩個不平行的向量          都垂

              直,則    是平面E的一個法向量.一般而言,    是平面E的一個法向量時, k    也是E的一個法向量,其

              中k是任意非零向量.

                        空間坐標系中,若平面E有法向量    = ( a, b, c )且過點A( x₀, y₀, z₀ ),又點P在平面E上(如下圖),

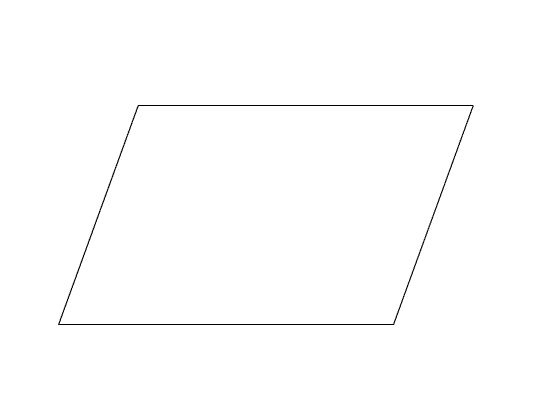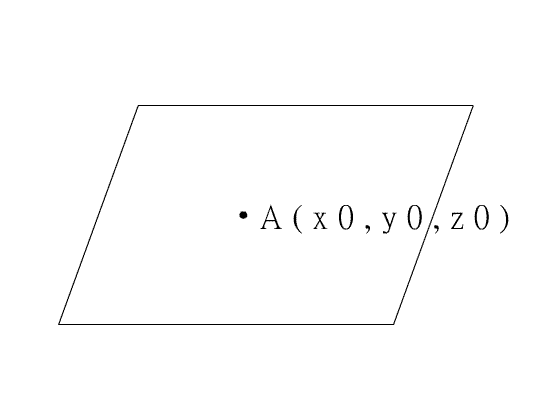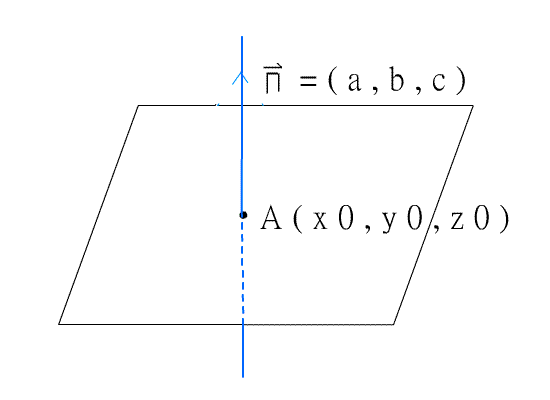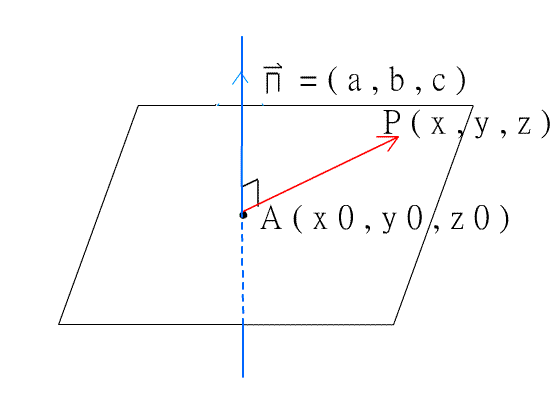
                     即

                     即

                     即

                      可得到

                      因此,平面E的方程式為

                      此式由一點及一法向量決定,故稱為平面的點向式,空間坐標系中,每一個平面都可由一個

              法向量    ,及平面上一點A( x₀, y₀, z₀),得其點向式,再化為ax+by+cz+d=0,其中d= - ( ax₀+by₀+cz₀ ),

              且a,b,c不皆為零,故每一個平面皆為某一個三元一次方程式的圖形

[上一頁]