2. 空間坐標系
空間中的一個平面E,如果建立了直角坐標系,以O為原點,兩軸是x軸與y軸,那麼此平面
上每一點都有一個實數對(x,y)作為坐標.如下圖一.若將此平面想成水平面,不在水平面上的
點,一定在此水平面的上方或下方,為了顯示此點離水平面的高度,我們增加一垂直於水平面
的直線坐標.通過原點O作水平面的垂直線,定為z軸,並在z軸建立另一直線坐標系,這三個軸
稱為坐標軸,其中原點仍為O,如此z軸與x軸,y軸都互相垂直,而形成空間中的另一直角坐標系
,O稱為此坐標系的原點.x軸與y軸所決定的平面稱為xy平面,同樣的,亦有yz平面與zx平面,這
三個平面都稱為坐標平面,如下圖二.


圖一 圖二
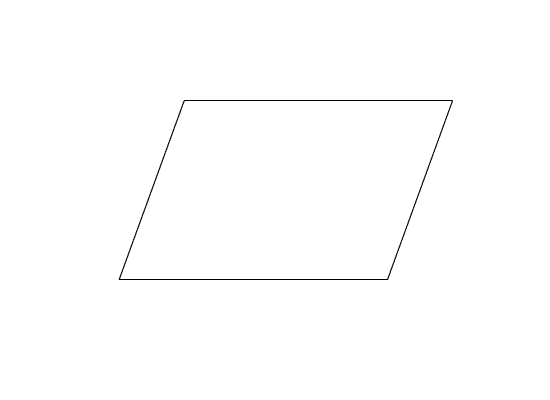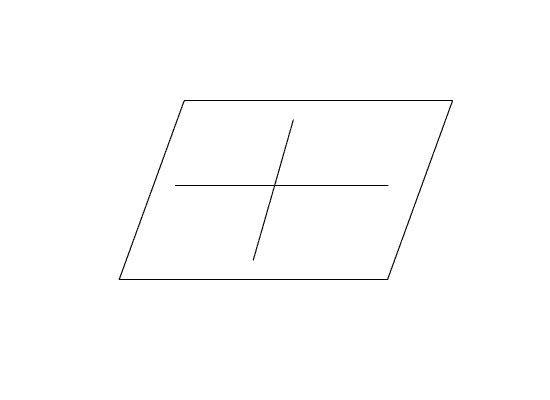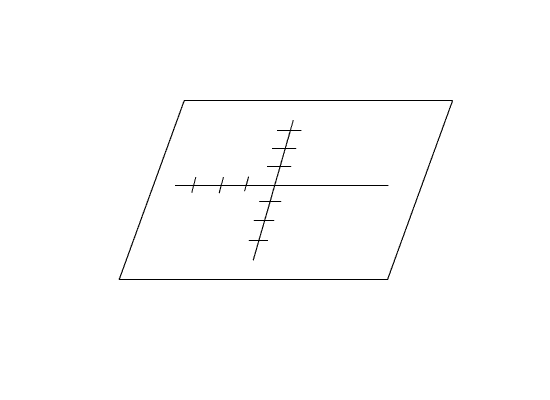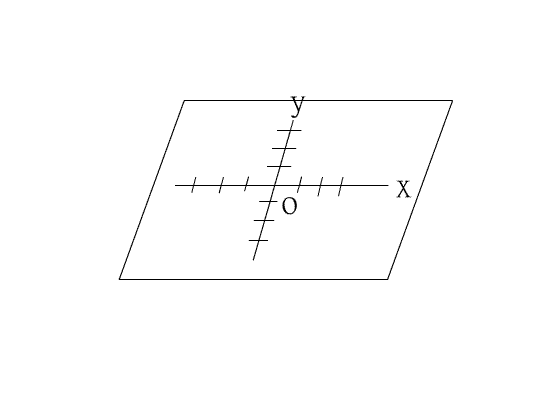
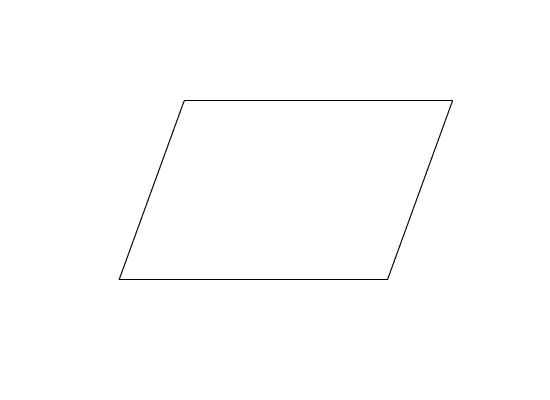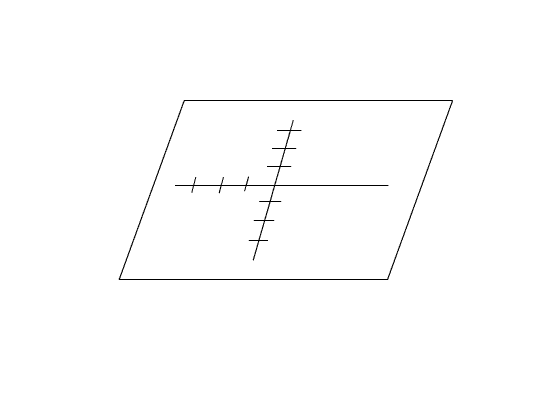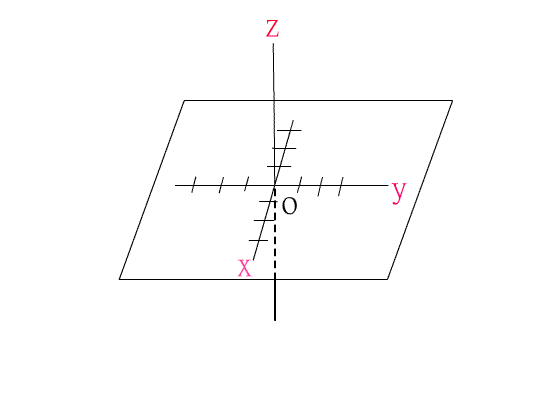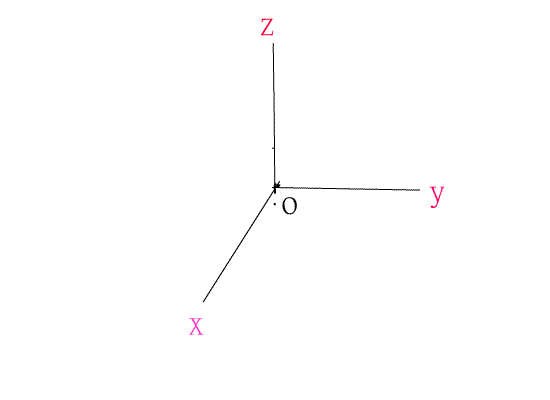
空間中,若過一點P作一直線L的垂直線,設交點為Q,則稱Q點為點P在直線L上的投影點;
若過一點P作一平面E的垂線,設交點為Q,則稱Q點為點P在平面E上的投影點.空間坐標系中,
一點P的空間坐標可如先前所說的方式決定,即考慮P點在xy平面上的投影點Q,設Q點在xy平
面上的的坐標為(a,b),再考慮P點在z軸上的投影點C,設C點在z軸上的直線坐標為c,則P點的空
間坐標為(a,b,c),記為(a,b,c),其中a,b,c分別為P點的x坐標,y坐標,z坐標.如下圖三.
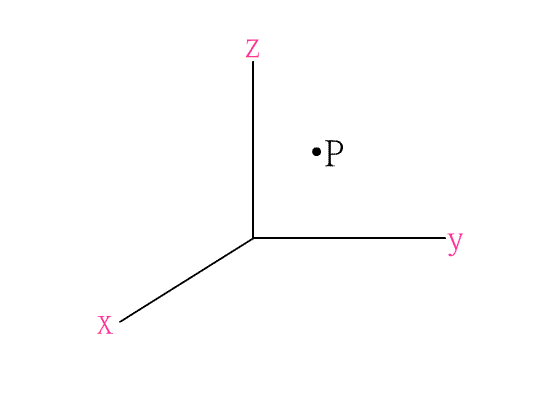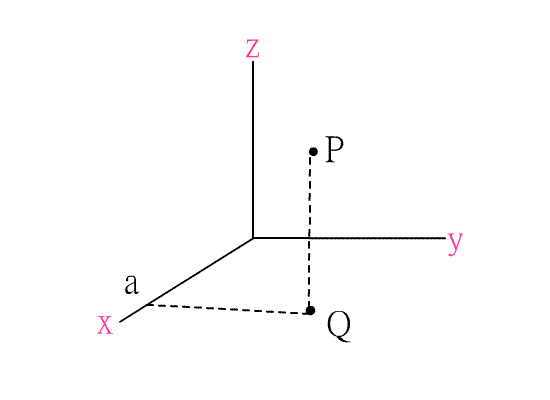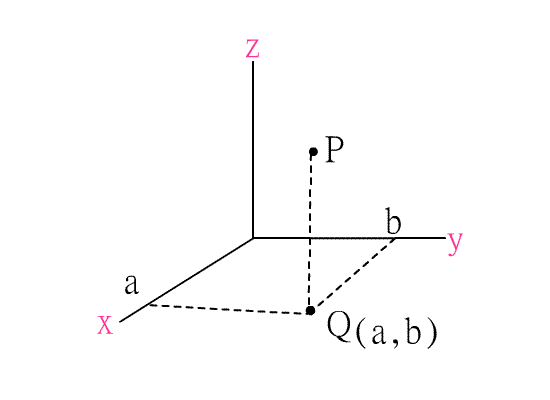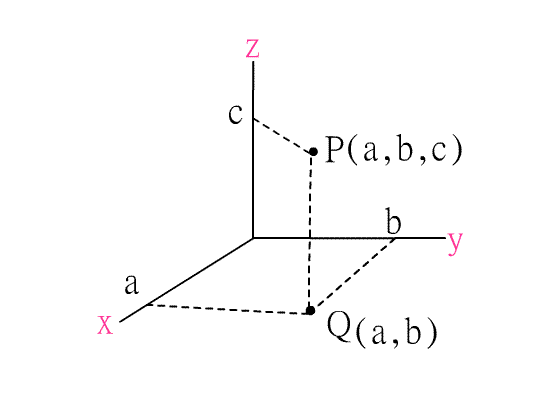
圖三 圖四
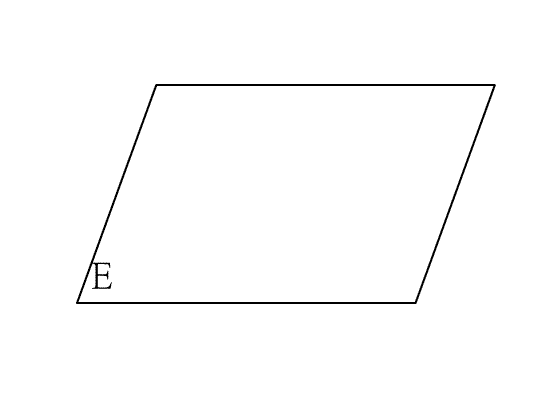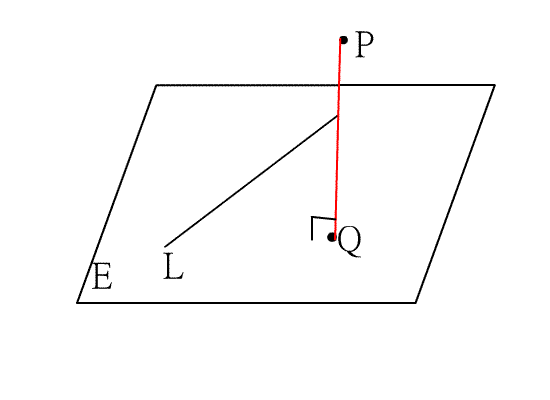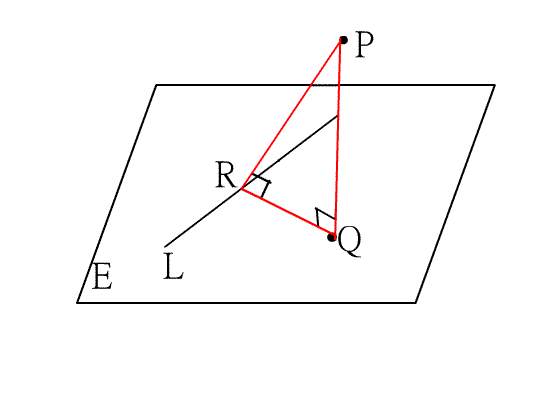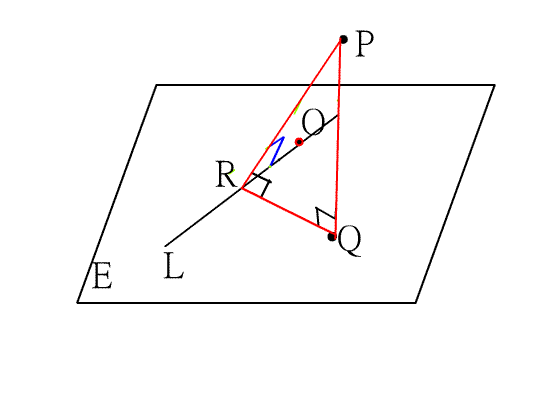
[ 三垂線定理]
若直線PQ垂直平面E於Q點,且直線QR垂直平面E上的直線L於R點,則直線PR與直線L垂直.如圖四.
<證明>
假設O是直線L上異於R的一點
![]()
由
![]()
![]()
![]()
由此得知
![]()
![]()
![]()
因此
![]()