當兩平面交於一直線L,此時,有四個像講義夾的圖形(如下圖一),每一個都稱為二面角,

             其中, θ就是此二面角的夾角.換言之,若P是直線L上一點,A,B分別是平面E1,E2上的點,且  

            

                    當直線L與平面E交於一點P,若平面E上,每一條過點P的直線都與L垂直,則稱直線L

               與平面E垂直.

                    

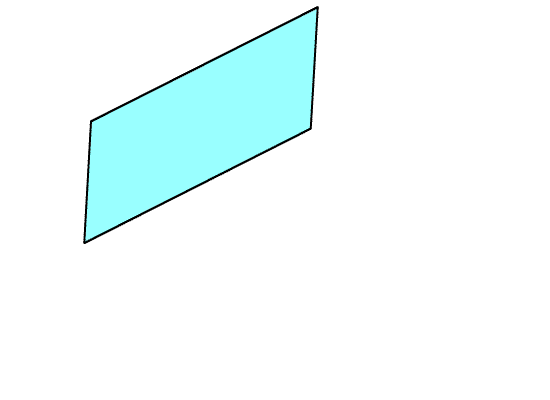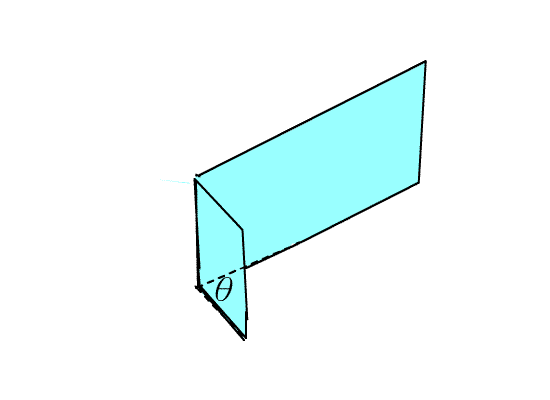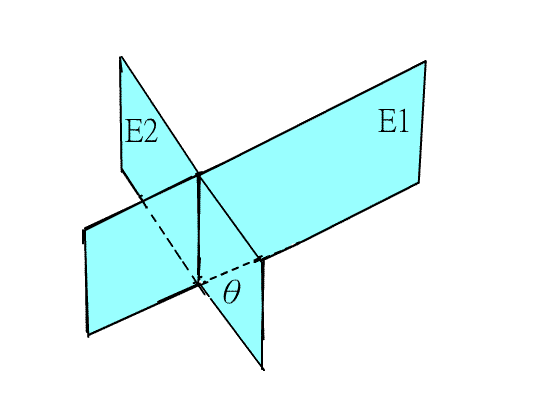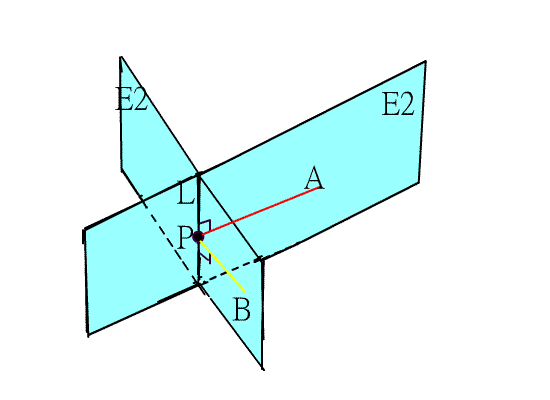
　                                     圖一                                                                                     圖二

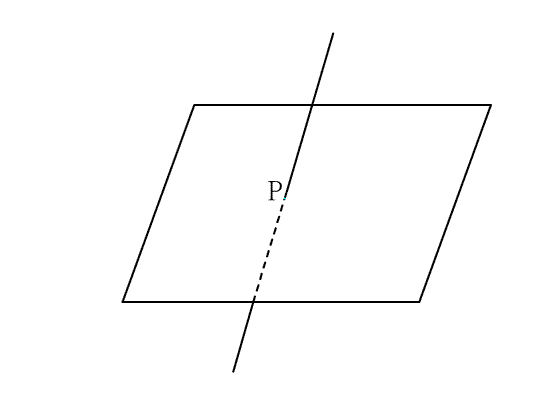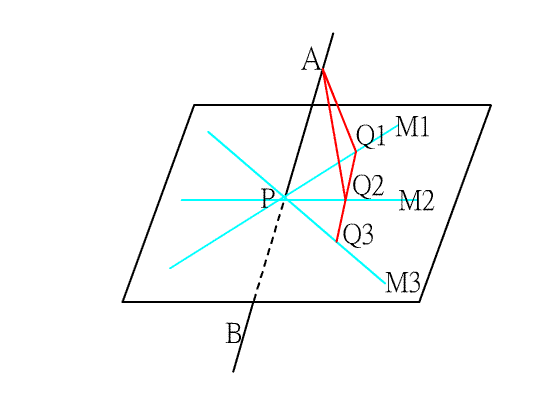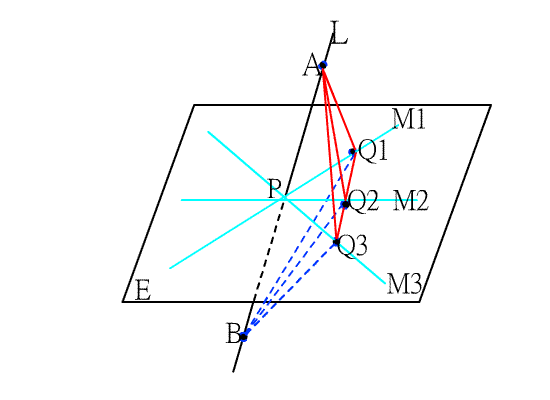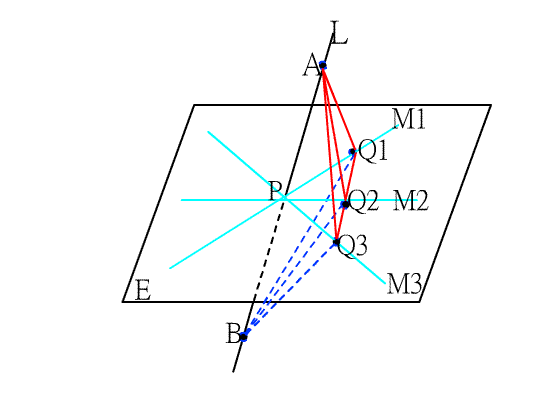
                  <說明>    如上圖二  

                                  在直線L上取兩點A,B,使P點為       的中點,又在直線M1,M2,M3上分別取Q1,Q2,Q3,

                                  使這三點在一直線上,由垂直平分線性質知

                                 

                                                         

                                  得到  

                                                                         

                                  故                             

                                                                   

                                  又得到

                                                                    

                                  故

                                                                          

                                   因此M3是        的垂直平分線

                                   所以

                                                                        

　

　                                由此可知,直線L與平面E交於一點P時,只要L與平面E上過P點的兩條直線垂直,

                                    就會與平面E上每一條過P點的直線垂直,也就是直線L與平面E垂直.

　

                                                                                     [上一頁]