情境模擬-教學活動二

教學活動二之課前準備情境模擬—前一堂課

老師：下一堂課要教的主題為利用加減消去法解二元一次聯立方程式，各位同學回家記得複習代入消去法，才能較快的進入狀況。

老師：同樣於下堂課一開始時，需要請四位學生上台來演一齣戲，角色分別有：旁白、富翁、管家、大盜；有沒有同學自願的？

學生：（舉手）或（沈默）

老師：如果沒有自願的同學我們就用抽籤決定。

【選定好四位學生後，將劇本發給選定的四位同學。】

老師：被選定演出的同學要於上課前先行演練。下課！

教學活動二之情境模擬

【先分組，依學生人數分組，每組約4人。】

【由課前準備的同學上台演出"誰是百變大盜-二部曲-失眠的管家"第一幕。("失眠的管家"劇本)】

老師：三位同學表演的很好，現在每一小組開始討論管家應該如何擺放寶石，可以利用每組的小道具輔助思考，並且將結果寫下。

學生：（討論中）

老師：現在請每組派一人，來將小組的結果畫到黑板上，並對全班同學說明。

【小組發表討論結果】

老師：現在我們來看看有沒有小組答對，正確答案：每個角落與牆邊皆擺放3顆寶石。

【以二元一次方程式方式解答】

老師：剛剛求答案時，大多數同學都是慢慢試出來，會花較多時間，而且也不一定可以解答出正確答案，很多時候我們可以利用已有的數學知識來解決問題，將會增加解題的速度及正確性，以這題來說，可以使用二元一次聯立方程式來解答。

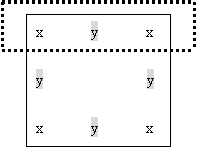
老師：假設每個角落擺x顆寶石（配合圖一說明）、每個牆邊擺放y顆寶石（配合圖二說明），共有4個角落與4個牆邊，而寶石共有24個，（配合圖三說明），可列出4x+4y=24 的式子。富翁睡前要檢查一邊為9顆寶石，一邊為2個角落與1個牆邊，（配合圖四說明），因此可列出：2x+y=9的式子。就得到了一個二元一次聯立方程式：4x+4y=24 為第(1)式，2x+y=9為第(2)式。

角 角 角 角		x x x x

圖一：

邊 邊 邊 邊		y y y y

圖二：

角 邊 角 邊 邊 角 邊 角		x y x y y x y x

圖三：

得到：4x+4y=24 …..(1)

		其中一邊：2x+y=9

圖四：

老師：現在問題就變成解二元一次聯立方程式：，現在同學利用上一堂課所教的「代入消去法」來解出答案。

學生：（埋頭計算）

老師：算出來的答案為多少？

學生：x=3、y=3。

老師：對，現在接著教一個解二元一次聯立方程式的新方法，「加減消去法」；「加減消去法」簡單的說就是要將消除其中一個變數（x或y），要消除哪一個變數，必須視題目而定，以能簡單的求的解為主，，消除哪一個變數，並沒有對錯。此題為例，我們可以消去變數x，則

Step1：(2)*2，將第二式乘2，得：4x+2y=18……(3)；一個方程式中的各項一起乘（或除）相同的任何數時，並不會影響這方程式的解，也就是說，

(2) 2x + y = 9………………(2)

(2)*2 4x + 2y = 18……………(3)

(2)*10 20x + 10y = 90………....(4)

(2)/2 x + 0.5y = 4.5………….(5)

上面(2)、(3)、(4)、(5)方程式的解均相同。

Step2：

Step3：(1)-(3)，第一式減第三式，得：2y=6，y=3

Step4：y=3代入第(2)式，得：2x+(3)=9，2x=6，x=3。

老師：最後我們求出二元一次聯立方程式：的解x=3、y=3，所以也就是每個角、邊都擺三顆寶石。

老師：不論利用「代入消去法」或「加減消去法」所求的答案皆相同，要使用哪一種方法來求解，必須依題目而定。

【學生繼續演出"失眠的管家"第二幕。("失眠的管家"劇本)】

老師：謝謝這四位同學生動的演出；現在要請各小組就戲劇中提到偷走寶石的問題開始討論，百變大盜是如何偷走4顆寶石，卻又沒讓富翁發現？並且將小組討論結果寫下。

學生：（小組討論）

老師：現在請每組派跟剛剛不一樣的同學上台，將小組的結果畫到黑板上，並對全班同學說明。

【小組發表討論結果】

老師：現在我們來看看有沒有小組答對，正確答案：每個角落放4顆、牆邊放1顆寶石。

老師：上述問題同樣可以使用二元一次聯立方程式來解答：假設每個角落擺x顆寶石、每個牆邊擺放y顆寶石，而寶石少了4顆，只剩20個，可列出4x+4y=20 的式子。富翁檢查每一邊為9顆寶石，可列出：2x+y=9的式子。就得到了一個二元一次聯立方程式：4x+4y=20 為第(1)式，2x+y=9為第(2)式。

老師：所以現在問題變成解二元一次聯立方程式：，現在同學利用剛剛所教的「加減消去法」來解出答案。

學生：（埋頭計算）。

老師：答案是多少？

學生：x=4、y=1。

老師：老師再講解一次，以加深同學的印象，這次也消去變數x，

Step1：(1)/2，將第二式除2，得：2x+2y=10……(3)

Step2：

Step3：(3)-(2)，第三式減第二式，得：y=1。

Step4：y=1代入第(2)式，得：2x+(1)=9，2x=8，x=4。

老師：最後我們求出二元一次聯立方程式：的解x=4、y=1，所以也就是每個角放置4顆珠寶、邊擺1顆寶石，這樣就可以輕鬆偷走四顆寶石。

【學生練習用加減消去法解類似的二元一次聯立方程式的題目】

老師：現在大家做做課本中帶入消去法的的練習。